Dois dados, um vermelho e outro azul, são lançados ao acaso. Sabendo-se que a soma obtida vale 6, a probabilidade de o número 2 ter aparecido em um dos dados é de:
O Serviço de Atendimento ao Cliente (SAC) de uma empresa registra as reclamações recebidas por e-mail, telefone ou fax. Observando o número de reclamações diárias em um período de 20 dias, o SAC concluiu que o número de dias (Xi) em que ocorreram i reclamações (i = 0,1,2,3,4,5) é dado por:
O valor da soma entre a mediana e a moda do número de reclamações (variável Xi) no período de 20 dias é igual a
Foram testados 64 microondas com desvio padrão de 2 anos e duração de vida média de 9 anos. O intervalo de
confiança de 90% para a média, sabendo que Z097, = 1,96 e Z095 = 1,64, é igual a:
Os valores da hora de trabalho, em reais, de oito funcionários de uma empresa estão descritos no quadro abaixo:
O valor da hora média, o valor da hora modal e o valor da hora mediana, em reais, são respectivamente:
Considere que a quantidade de chocolate, em gramas, em panetones tenha distribuição normal com média de 27,3 e desvio padrão 0,4. Selecionando, aleatoriamente, um panetone, a probabilidade de ele nele conter chocolate entre 27,18 g e 27,38 g é de:
A capacidade, em mililitros, de embalagens de leite é distribuída normalmente em torno de uma média de 320 ml e desvio padrão de 40 ml. Para determinar a probabilidade P(Z < 1,25) é necessária uma capacidade, em mililitros, de:
Na fabricação de um produto por um empresa verificou–se uma taxa de 0,2 defeitos por unidade. Com base na distribuição de Poisson, se for escolhido um produto qualquer, a probabilidade de esse produto apresentar exatamente um defeito é aproximadamente igual a: [Considere e–0,2 = 0,82].
O gráfico indica o nível de escolaridade retirada de uma amostra dos habitantes de uma cidade.
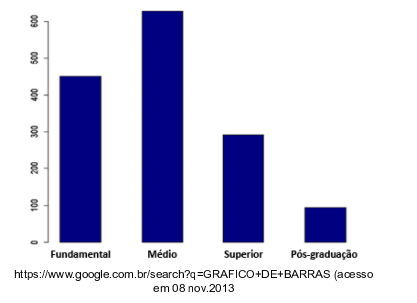
De acordo com os dados da tabela, considerando uma população de 150.000 pessoas, é correto afirmar que o
percentual de pessoas com nível superior e pós–graduação dessa cidade é:
A fórmula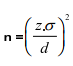
é utilizada para a seleção do tamanho de uma amostra aleatória simples de uma população
infinita, z representa a abscissa da distribuição normal, d o erro amostraL e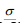 
o desvio padrão da população.
O tamanho de uma amostra aleatória simples de parafusos, com um nível de confiança de 95% , supondo uma
população infinita de parafusos cuja variável é o "peso" em gramas, com variãncia igual a 25g2, e um erro amostrai
de 0,14g, deve ser um número:
[Nível de confiança: 0,95 (z = 1,96) ; 0,955 (z = 2) ; 0,99 (z = 2,57)]
Considere os seguintes cálculos para a média de n valores denotados por x1, x2, ... xn nos quais w1, w2, ... wM são constantes positivas.
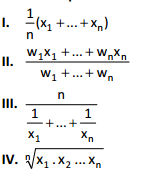
As médias aritméticas simples, aritmética ponderada,
geométrica e harmônica são calculadas, respectivamente,
por
Considere o teste T para testar a hipótese nula de que µ, a
média de uma variável aleatória com distribuição Normal,
seja igual a 0 (zero), usando o nível de significância igual a
0,05. É INCORRETO afirmar que
Um grupo de 100 alunos, sendo 50 meninos e 50 meninas,
todos da mesma faixa etária e cursando o mesmo ano
escolar, responderam a um questionário sobre métodos
anticoncepcionais. O objetivo do estudo era verificar se a
proporção de alunos com conhecimento adequado sobre
anticoncepção é homogênea nos dois gêneros. Para ter um
conhecimento considerado adequado, o aluno deveria
acertar todas as questões. Ao final da correção de cada
questionário, registrava-se o acerto ou não das perguntas.
Os resultados foram resumidos e apresentados na tabela a
seguir.
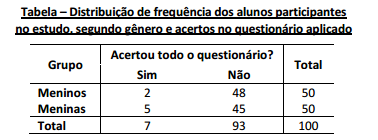
Considerando o desenho do estudo, o tipo de variável
observada e os dados obtidos, o teste estatístico mais
adequado para avaliar a hipótese de estudo é o
Pesquisadores da área da saúde cardiovascular pretendem
descobrir se um tratamento para diminuir o nível de
colesterol no sangue sofre influência do gênero do paciente.
Para isso, selecionaram um grupo de voluntários de
ambos os sexos e coletaram dados sobre as variáveis
clínicas relacionadas na tabela abaixo.
Considerando as estatísticas descritivas (média e desviopadrão)
divulgadas na tabela, analise.
I.As mulheres são mais homogêneas na variável IMC do
que na variável Colesterol Total.
II.Os homens são mais homogêneos na variável Peso do
que na variável IMC.
III.Tanto para mulheres quanto para homens, a variável
com medidas mais heterogêneas é o Colesterol Total.
Está(ão ) correta(s ) apenas a(s ) afirmativa( s)
Marque V para as afirmativas verdadeiras e F para as
falsas.
( ) Para ajustar um modelo ARIMA, é necessário considerar
os estágios de identificação e estimação.
( ) Um processo autorregressivo de ordem p tem a função
de autocovariância decrescente, na forma de exponenciais
ou senoides amortecidas, finitas em extensão.
( ) Um processo de médias móveis de ordem q tem função
de autocovariância finita, apresentando um corte após
o “lag" q.
( ) Um processo autorregressivo e de médias móveis de
ordem (p, q) tem função de autocovariância infinita em
extensão, que decai de acordo com exponenciais e/ou
senoides amortecidas após o “lag" q-p.
( ) Após a identificação provisória de um modelo de séries
temporais, pode-se usar os métodos de mínimos quadrados
ou de máxima verossimilhança, entre outros,
para estimação dos parâmetros. Os estimadores obtidos
pelo método dos momentos não têm propriedades
boas quando comparadas com os dois já mencionados.
Entretanto, podem ser utilizados para gerar os valores
iniciais nos processos iterativos.
A sequência está correta em
O modelo de análise fatorial representa a estrutura de covariância
entre muitas variáveis aleatórias X´ = [X1 , X2, ∙∙∙, Xp],
através de poucas variáveis não observáveis F´ = [F1, F2 , ∙∙∙,
Fm ] também conhecidas como fatores, construtos ou fatores
comuns. Sendo E( X) = μ e V(X ) = Σ, o modelo fatorial é
expresso por X – μ = LF + ε. A matriz Lpmx
é conhecida como matriz das cargas fatoriais e seus elementos, lij , carga da
variável i no fator j e as variáveis aleatórias F e εm + p são não observáveis. Analise as afirmativas, marque V para as
verdadeiras e F para as falsas.
( ) No modelo fatorial ortogonal, as variáveis não observá-
veis F e ε são independentes, E(F ) = 0, V(F ) = E(F´F) = I,
E(ε ) = 0, V(ε ) = E(ε´ε) = Ψ. A matriz Ψ é não diagonal,
V(X ) = Σ = L´L + Ψ e Cov (X, F) = L.
( ) Um método de estimação para as cargas do modelo
fatorial ortogonal é através de componentes principais,
onde se utiliza a decomposição espectral da matriz Σ.
( ) Para se utilizar o método de máxima verossimilhança
para estimar as cargas, é acrescida a suposição de que
F e ε têm distribuição normal multivariada. As comunalidades
(elementos da diagonal LL´) têm como estimadores
a proporção da variância total estimada pelo
particular fator.
( ) Para melhorar a explicação do modelo fatorial, sem
alterar a ortogonalidade dos fatores, muitas vezes, usase
uma transformação ortogonal das cargas fatoriais,
que, consequentemente, transforma os fatores. Esse
procedimento é conhecido como rotação fatorial.
( ) Dependendo da natureza dos dados, os fatores não
precisam ser ortogonais. Assim, para melhorar a explicação
do modelo fatorial, pode-se utilizar a rotação
oblíqua, onde cada variável é expressa em termos de
um número máximo de fatores.
A sequência está correta em
