No que concerne a união e intersecção de eventos, julgue os itens que se seguem
No que concerne a união e intersecção de eventos, julgue os itens que se seguem
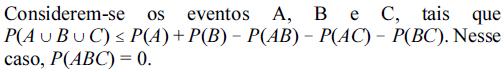
Um estudo sobre a informalidade no mercado de trabalho mostrou
que o número X de empregados não registrados por microempresa
segue uma distribuição binomial negativa na forma
P(X = k) = (k + 1)p2(1 p)k, em que k = 0, 1, 2, ... e o parâmetro p
dessa distribuição é tal que 0 < p < 1. Com base nessas informações
e considerando a média amostral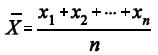 
em que X1, X2, ..., Xn representa uma amostra aleatória simples retirada
dessa distribuição, julgue os itens a seguir.
O estimador de máxima verossimilhança da média populacional é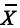 
.
Considerando que o número mensal Y de acidentes de trabalho siga
uma distribuição de Poisson com média m e que a tabela acima
apresente a realização de uma amostra aleatória simples de tamanho
n = 100, retirada da população Y, julgue os itens subsecutivos.
Por máxima verossimilhança, estima-se que o valor de m seja igual a 0,7.
Considerando que as propriedades da estatística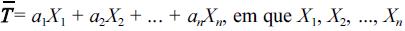 
representa uma
amostra aleatória simples de tamanho n, retirada de uma população
X com média µ, e que a1, a2, ..., an, são constantes positivas tais que
a1+a2+an= 1, julgue os itens que se seguem.
O erro padrão da estatística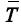 
é igual 
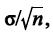a em que s representa o desvio padrão da população X.
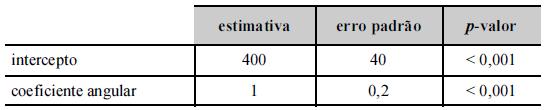
Um modelo de regressão linear simples foi ajustado pelo
método de mínimos quadrados ordinários como parte de um laudo
de avaliação imobiliária. Nesse modelo, cujos resultados se
encontram na tabela acima, a variável resposta y representa
o valor do imóvel, em R$ mil, e a variável regressora x é a
área construída do imóvel (em m2+a).
Considerando que o tamanho da amostra para essa modelagem
tenha sido superior a 500 e que os erros aleatórios pertinentes sejam
normais, julgue os itens a seguir.
A distribuição amostral do estimador do coeficiente angular se relaciona com uma distribuição t de Student com 498 graus de liberdade.
Um modelo de regressão linear múltipla, que foi ajustado em uma perícia judicial, possui 11 variáveis explicativas. O tamanho da amostra nessa modelagem foi igual a 101. A soma de quadrados total foi igual a 15.000 e a soma de quadrados residual foi igual a 5.000. Com base nessas informações, julgue os próximos itens.
O quadrado médio dos erros (mse) é superior a 50.
Um modelo de regressão linear múltipla, que foi ajustado em uma perícia judicial, possui 11 variáveis explicativas. O tamanho da amostra nessa modelagem foi igual a 101. A soma de quadrados total foi igual a 15.000 e a soma de quadrados residual foi igual a 5.000. Com base nessas informações, julgue os próximos itens.
A soma de quadrados do modelo de regressão é inferior a 12.000.
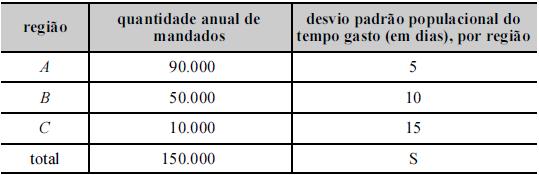
Um levantamento estatístico por amostragem probabilística
foi realizado para se estimar o tempo médio, em dias, gasto por
oficiais de justiça no cumprimento de mandados judiciais. Nesse
levantamento, os mandados foram divididos de acordo com a
localização geográfica do intimado. A tabela acima mostra a
quantidade anual de mandados para cada região, os valores dos
desvios padrão da variável de interesse por região e S, que
representa o desvio padrão populacional do tempo gasto.
Considerando que o total de mandados judiciais utilizados no
levantamento tenha sido igual a 400, julgue os itens de
Considerando-se a amostragem aleatória estratificada com
alocação proporcional ao tamanho dos estratos, a quantidade
de observações no estrato A será igual a 240.
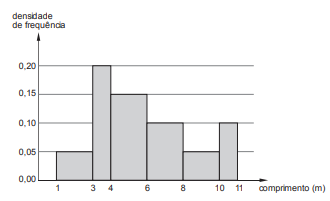
A distribuição das medidas em metros (m) dos comprimentos dos cabos no estoque de uma fábrica está representada pelo histograma mostrado abaixo, em que no eixo vertical constam as densidades de frequências, em (m)-1, e no eixo horizontal os intervalos de classe. Define-se densidade de frequência de um intervalo de classe como sendo o resultado da divisão da respectiva frequência relativa pela correspondente amplitude do intervalo.
Sabendo-se que todos os intervalos de classe são fechados à esquerda e abertos à direita, então a porcentagem dos cabos que apresentam uma medida de comprimento de pelo menos igual a 4 m e inferior a 10 m é de
Considere uma variável aleatória X uniformemente distribuída no intervalo (m, n) em que nem m e nem n são conhecidos. Com base em uma amostra aleatória de tamanho 10 obteve-se que os valores do primeiro e do segundo momentos da amostra foram, respectivamente, 1,00 e 1,12. Aplicando o método dos momentos, tem-se que as estimativas de m e n são, respectivamente,
Então, utilizando as informações dos dados acima, é correto afirmar que H0
Uma variável aleatória X tem distribuição Binomial com parâmetros n = 200 e p = 0,01. Fazendo uso da aproximação de Poisson à binomial, a probabilidade de X ser maior do que zero é igual a 0,865. Nessas condições, a probabilidade de X ser igual a 5, calculada pela aproximação de Poisson à binomial, é
Seleciona-se aleatoriamente um funcionário, dentre os funcionários que realizam a tarefa no órgão público. A probabilidade dele realizar a tarefa em menos do que duas horas é
