De uma população com 100 elementos que tem variância σ2 = 49, tomou-se uma amostra aleatória simples, sem reposição, de tamanho n. Sabe-se que a média amostral dessa amostra tem variância igual a 217⁄33. Nessas condições, o valor de n é
Em uma pescaria, os pescadores Alberto, Bruno e Carlos
colocavam os peixes que pescavam em um mesmo recipiente. Ao
final da pescaria, o recipiente continha 16 piaus e 32 piaparas. Na
divisão dos peixes, cada um deles afirmou que teria pescado mais
peixes que os outros dois.
Julgue os itens a seguir, a respeito dessa situação.
Na situação dada, se, mediante um acordo, cada pescador ficasse com a mesma quantidade de peixes 16 peixes e, do total de peixes de Alberto, 3 fossem piaus, então a quantidade de maneiras de se dividir os peixes entre Bruno e Carlos, de modo que cada maneira resultasse em uma quantidade diferente de piaparas para Carlos, seria menor que 15.
Com base nos conceitos de probabilidade, julgue o item seguinte.
Se três eventos (A, B e C) formam uma partição do espaço amostral com P(A) = P(B) = 1⁄4, então P(C) > 1⁄3.
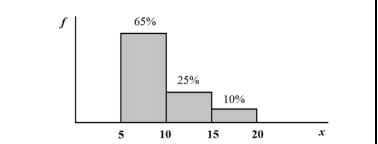
Com referência à figura acima, que mostra a distribuição da renda
mensal — x, em quantidades de salários mínimos (sm) — das
pessoas que residem em determinada região, julgue os itens
subsequentes.
A variável x, por possuir quatro níveis de respostas, é do tipo qualitativa ordinal.
Pedro e João são os oficiais de justiça no plantão do fórum
de determinado município. Em uma diligência distribuída a Pedro,
X é a variável aleatória que representa o sucesso (X = 1) ou
fracasso (X = 0) no cumprimento desse mandado. Analogamente,
Y é a variável aleatória que representa o sucesso (Y = 1) ou
fracasso (Y = 0) de uma diligência do oficial João.
Com base nessa situação hipotética e considerando a soma
S = X + Y, e que P(X = 1) = P(Y = 1) = 0,6 e E(XY) = 0,5, julgue
os itens que se seguem, acerca das variáveis aleatórias X, Y e S.
A variável aleatória S segue uma distribuição binomial com parâmetros n = 2 e p = 0,6.
Um estudo acerca da qualidade dos serviços prestados por um
cartório considerou os indicadores X e Y. A análise de regressão
linear produziu as retas ajustadas (por mínimos quadrados
ordinários) Com relação a esses
indicadores, julgue os itens que se seguem.
A média amostral do indicador Y é igual a 10

Um estudo foi realizado para avaliar a associação linear entre o
valor de uma causa judicial trabalhista (Y) e o seu tempo de duração
do processo (X). Considerando o modelo de regressão linear
simples na forma Yi = aXi + b + εi , em que εi representa o erro
aleatório normal com média nula e variância V, a tabela acima
mostra alguns resultados. Com base nessas informações,
considerando que â representa a estimativa de mínimos quadrados
ordinários do coeficiente angular desse modelo de regressão linear,
julgue os próximos itens.
O valor do coeficiente do R2 ajustado é superior a 0,7
Considere que a amostra aleatória simples X1, X2, ..., Xn tenha sido
retirada de uma distribuição exponencial com função de densidade
na forma f(x) = γexp(–γx), em que x > 0 e γ > 0. Com relação a essa
amostra e à inferência estatística, julgue os itens que se seguem.
A soma
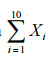
é uma estatística suficiente para a estimação do parâmetro γ
Julgue os itens seguintes, relativos às técnicas de amostragem
Considerando os estimadores y = média amostral;

Com referência à estatística computacional, julgue os itens
subsequentes.
Considere que um experimento consista em gerar uma amostra de tamanho n de uma distribuição de média μ e variância σ2 e que, para cada 1.000 amostras de tamanho n, toma-se o quantil de ordem 95% da distribuição da média das amostras. Nesse cenário, se K(n) for o resultado do experimento para amostras de tamanho n, então a distribuição assintótica de K(n) será uma distribuição normal.
No que concerne aos processos estocásticos, julgue os itens
seguintes.
Se, em um processo de Markov em tempo discreto, a matriz de transição for M, e se v for o vetor distribuição estacionária do processo, então vM2 = vM100.
Julgue os itens a seguir, relativos à análise multivariada.
Na análise fatorial, a rotação varimax, que não é ortogonal, tem por objetivo maximizar a variância das cargas fatoriais.
Julgue os itens a seguir, relativos à análise multivariada.
Considere que, na análise discriminante por meio do escore quadrático, o vetor x seja classificado na população k se

Considerando a sequência 2; 4; 3; 2; 7; 6, uma média móvel de ordem 2 pode ser dada pela sequência
Dada a sequência de números: 71; 24; 36; 10; 12; 41; 52, o número que define o 3º quartil é

