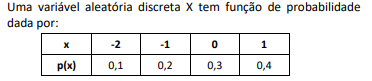
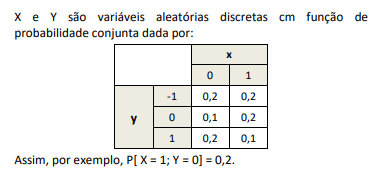
Uma urna I contém inicialmente 4 bolas azuis e 6 bolas vermelhas; nessa ocasião, a urna II contém 5 bolas azuis e 4 bolas vermelhas, e a urna III, 2 azuis e 7 vermelhas.
Uma bola é sorteada da urna I e colocada na urna II. Em seguida, uma bola é sorteada da urna II e colocada na urna III. Por fim, uma bola é sorteada da urna III.
A probabilidade de que a bola sorteada da urna III seja azul é igual a
Se (Xn) é uma sequência de variáveis aleatórias com distribuição uniforme no intervalo (0, (n – 1)/ n), n > 1, então (Xn) converge para uma distribuição
Se X1, X2, ..., Xn é uma amostra aleatória simples de uma distribuição exponencial com parâmetro θ, ou seja,
f(x|θ) = θe-θx, θ > 0,
então, o estimador de θ pelo método dos momentos é
Uma amostra aleatória simples de tamanho 400 foi obtida de uma variável aleatória populacional, com média µ desconhecida e apresentou os seguintes resultados:
Média amostral: 125
Variância amostral: 100
Um intervalo aproximado com 95% de confiança para µ será dado por
Uma variável aleatória populacional tem média desconhecida e variância 25. O tamanho da amostra aleatória simples para que possamos garantir, com 95% de confiança, que o valor da média amostral não se afastará do da média populacional por mais de 0,2 unidade, deve ser maior ou igual a
Se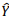 
= b0 + b1X é a reta ajustada pela regressão e se ei = Yi - 
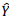é o resíduo da observação i, i – 1, ..., n, avalie as afirmativas a seguir.
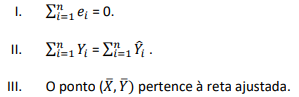
Está correto o que se afirma em
O segmento de reta com extremidades no ponto P(5,0) e no centro da circunferência (x - 1)2 + (y - 3)2 = 4 intersecta a circunferência no ponto Q.
A distância de P até Q mede
Uma reta com coeficiente angular 3 intersecta uma reta com coeficiente angular 5 no ponto (5, 23).
A área do triângulo que essas retas formam com o eixo das ordenadas é
Considere a função real f definida por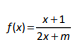 
e sua inversa f -1 .
Se f-1(2) = 5 , o valor de m é
Se 1002x . 10003x = 1004, então o valor de x é
A figura a seguir mostra a secante PAB e a tangente PT a uma circunferência. Sabe-se que, no triângulo PTB, tem-se PT = TB e que, na circunferência, os arcos AB e BT têm a mesma medida.
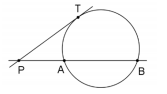
O ângulo APT mede
O quadrado ABCD tem lado de 2 unidades. Uma circunferência passa pelos pontos A e B e é tangente ao lado CD.
O raio dessa circunferência mede
Uma pirâmide quadrangular regular tem altura 30 e aresta da base também igual a 30.
A distância do centro da base dessa pirâmide a uma das suas faces laterais é
