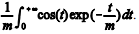Para um estudo sobre a gestão de riscos jurídicos em determinado tribunal, um analista efetuará simulações de Monte Carlo com base em realizações de variáveis aleatórias contínuas Y (exponencial, com média m), U (uniforme no intervalo [0,1]) e Q (qui-quadrado, com k graus de liberdade).
Considerando que
Y, U e Q sejam mutuamente independentes, julgue o próximo item.
Suponha que Y1, Y2,..., Yn sejam n realizações independentes retiradas de uma distribuição exponencial com média m. Nessa situação, a média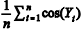 
representa uma estimativa da integral 
Todo paciente que chega a determinado posto hospitalar é imediatamente avaliado no que se refere à prioridade de atendimento. Suponha que o paciente seja classificado como "emergente" (Y = 0) ou como "não emergente" (Y = 1), e que as quantidades X, diárias, de pacientes que chegam a esse posto sigam uma distribuição de Poisson com média igual a 20. Considerando que W represente o total diário de pacientes emergentes, de tal sorte que
, em que 0 ≤ w ≤ x e x ≥ 0, julgue o item subsequente.
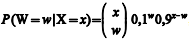
Se, em determinado dia, 10 pacientes forem atendidos nesse posto hospitalar, então a probabilidade de se registrar, entre esses pacientes, exatamente um paciente emergente será igual a 0,1.
Uma amostra aleatória simples
Y1, Y2, ..., Y25 foi retirada de uma distribuição normal com média nula e variância σ2, desconhecida. Considerando que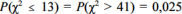 
, em que 
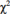representa a distribuição qui-quadrado com 25 de liberdade, e que 
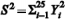, julgue o item a seguir.
A variância da distribuição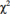 
, com 25 graus de liberdade é superior a 40.
Sabe-se que a distribuição geométrica pode ser interpretada como uma sequência de ensaios de Bernoulli, independentes, até a ocorrência do primeiro sucesso. Assinale a alternativa que indica corretamente a média e a variância, respectivamente, de uma distribuição geométrica cujo parâmetro é p = 0,64 e tendo como parametrização o número de ensaios de Bernoulli até se obter um sucesso.
Todo paciente que chega a determinado posto hospitalar é imediatamente avaliado no que se refere à prioridade de atendimento. Suponha que o paciente seja classificado como "emergente" (Y = 0) ou como "não emergente" (Y = 1), e que as quantidades X, diárias, de pacientes que chegam a esse posto sigam uma distribuição de Poisson com média igual a 20. Considerando que W represente o total diário de pacientes emergentes, de tal sorte que
, em que 0 ≤ w ≤ x e x ≥ 0, julgue o item subsequente.
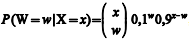
O total diário W de pacientes emergentes segue uma distribuição de Poisson com média superior a 3.
Os tempos de duração de exames de cateterismo cardíaco ( Y, em minutos) efetuados por determinada equipe médica seguem uma distribuição normal com média µ e desvio padrão σ, ambos desconhecidos. Em uma amostra aleatória simples de 16 tempos de duração desse tipo de exame, observou-se tempo médio amostral igual a 58 minutos, e desvio padrão amostral igual a 4 minutos.
A partir da situação hipotética apresentada e considerando Φ(2) = 0,977, em que Φ(z) representa a função de distribuição acumulada de uma distribuição normal padrão e z é um desvio padronizado, julgue o item que se segue, com relação ao teste de hipóteses H0 = µ ≥ 60 minutos, contra HA = µ < 60 minutos, em que H0 e HA denotam, respectivamente, as hipóteses nula e alternativa.
Ao se aplicar o teste t de Student com nível de significância igual a 2,3%, conclui-se haver evidências estatisticamente significativas contra a hipótese H0.
Uma amostra aleatória simples
Y1, Y2, ..., Y25 foi retirada de uma distribuição normal com média nula e variância σ2, desconhecida. Considerando que 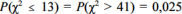, em que 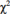representa a distribuição qui-quadrado com 25 de liberdade, e que 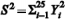, julgue o item a seguir.
A razão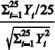 
segue uma distribuição t de Student com 24 graus de liberdade.
O toal diário – X – de pessoas recebidas em uma unidade de pronto atendimento (UPA) para atendimento ambulatorial, e o total diário – Y – de pessoas recebidas nessa mesma UPA para atendimento de urgência seguem processos de Poisson homogêneos, com médias, respectivamente, iguais as 20 pacientes/dia e 10 pacientes/dia, e as variáveis aleatórias X e Y são independentes. Sabe-se que, em média, a necessidade de cuidados hospitalares atinge 10% dos pacientes do atendimento ambulatorial e 90% dos pacientes do atendimento de urgência.
A partir dessa situação hipotética, julgue o próximo item, considerando que o registro da necessidade de cuidados hospitalares seja feito no momento em que o paciente chegue à UPA e que H seja a quantidade diária registrada de pacientes com necessidades de cuidados hospitalares.
A soma X + Y segue uma distribuição de Poisson com média e variância respectivamente iguais a 30 e 900.
Supondo que o custo unitário X de um processo de execução fiscal na justiça federal seja descrito por uma distribuição exponencial com média igual a R$ 5.000, julgue o próximo item.
A variável aleatória Y = e!X segue a distribuição Beta.
Supondo que o custo unitário X de um processo de execução fiscal na justiça federal seja descrito por uma distribuição exponencial com média igual a R$ 5.000, julgue o próximo item.
O coeficiente de variação de X é igual a 1.
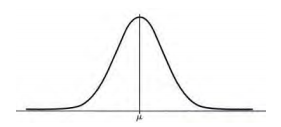
A variável normal padronizada Z é dada por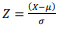 
, em que X é uma variável que tem distribuição normal de média μ e variância σ2, conforme a figura apresentada. Considerando uma variável X que tem distribuição normal de média μ = 15,6 e variância σ2 = 0,25, assinale a alternativa que indica a probabilidade p(15 < X < 16,2).
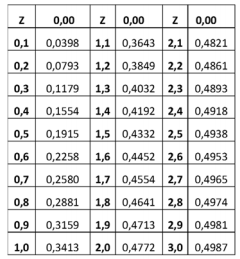
Dado: Tabela – Áreas de uma distribuição normal padrão
Todo paciente que chega a determinado posto hospitalar é imediatamente avaliado no que se refere à prioridade de atendimento. Suponha que o paciente seja classificado como "emergente" (Y = 0) ou como "não emergente" (Y = 1), e que as quantidades X, diárias, de pacientes que chegam a esse posto sigam uma distribuição de Poisson com média igual a 20. Considerando que W represente o total diário de pacientes emergentes, de tal sorte que
, em que 0 ≤ w ≤ x e x ≥ 0, julgue o item subsequente.
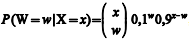
A curva de regressão de W em X = x é dada pela média condicional E(W|X = x) = 0,1x.
X1, X2, ..., X10 representa uma amostra aleatória simples retirada de uma distribuição normal com média µ e variância σ2, ambas desconhecidas. Considerando que 
e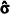 
representam os respectivos estimadores de máxima verossimilhança desses parâmetros populacionais, julgue o item subsecutivo.
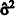é um estimador viciado (ou tendencioso) para a variância populacional, pois 
.
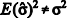X1, X2, ..., X10 representa uma amostra aleatória simples retirada de uma distribuição normal com média µ e variância σ2, ambas desconhecidas. Considerando que e 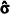representam os respectivos estimadores de máxima verossimilhança desses parâmetros populacionais, julgue o item subsecutivo.
O estimador de máxima verossimilhança para a função de densidade da distribuição normal em questão é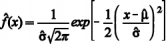 
, para qualquer valor real x.
Considerando que X e Y sejam variáveis aleatórias mutuamente independentes que seguem distribuição normal padrão, julgue o próximo item.
A soma dos quadrados Q = X2 + Y2 segue uma distribuição exponencial com média igual a 2.
