Uma amostra aleatória simples
Y1, Y2, ..., Y25 foi retirada de uma distribuição normal com média nula e variância σ2, desconhecida. Considerando que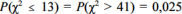 
, em que 
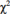representa a distribuição qui-quadrado com 25 de liberdade, e que 
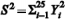, julgue o item a seguir.
[S 2/41;S2/13] representa um intervalo de 95% de confiança para a variância σ2.
O toal diário – X – de pessoas recebidas em uma unidade de pronto atendimento (UPA) para atendimento ambulatorial, e o total diário – Y – de pessoas recebidas nessa mesma UPA para atendimento de urgência seguem processos de Poisson homogêneos, com médias, respectivamente, iguais as 20 pacientes/dia e 10 pacientes/dia, e as variáveis aleatórias X e Y são independentes. Sabe-se que, em média, a necessidade de cuidados hospitalares atinge 10% dos pacientes do atendimento ambulatorial e 90% dos pacientes do atendimento de urgência.
A partir dessa situação hipotética, julgue o próximo item, considerando que o registro da necessidade de cuidados hospitalares seja feito no momento em que o paciente chegue à UPA e que H seja a quantidade diária registrada de pacientes com necessidades de cuidados hospitalares.
A quantidade diária H segue uma distribuição de Poisson.
Considerando que uma amostra aleatória simples X 1, X2, ..., Xn tenha sido retirada de uma população exponencial com média igual a 5, julgue os próximos itens, relativos à média amostral
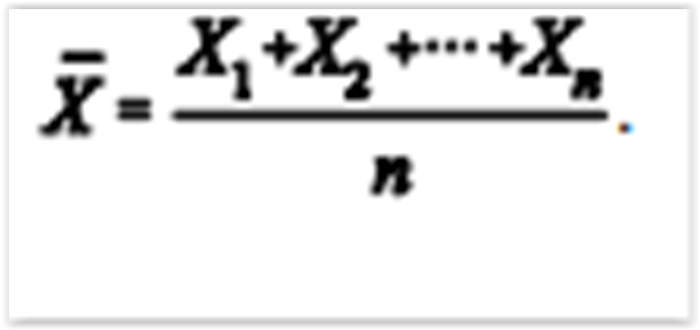
A variância da média amostral é igual a 25.
Em um determinado município, 70% da população é favorável a um certo projeto. Se uma amostra aleatória de cinco pessoas dessa população for selecionada, então a probabilidade de exatamente três pessoas serem favoráveis ao projeto é igual a
Considerando-se que apenas os 10% que atinjam as maiores notas serão aprovados, a nota mínima para aprovação é:
Uma amostra aleatória, com n = 16 observações
independentes e identicamente distribuídas (IID), foi obtida a partir
de uma população infinita, com média e desvio padrão
desconhecidos e distribuição normal.
Tendo essa informação como referência inicial, julgue os seguintes
itens.
Se a variância amostral for igual a 4,0, o erro padrão da média amostral será igual a 0,5
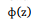Sabe-se que as notas de uma prova têm distribuição Normal
com média μ = 6,5 e variância α² = 4
. Adicionalmente, são
conhecidos alguns valores tabulados da normal-padrão.
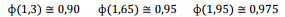
Onde,
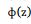é a função distribuição acumulada da Normal Padrão.
Considerando-se que apenas os 10% que atinjam as maiores notas
serão aprovados, a nota mínima para aprovação é:
Considere as seguintes distribuições de probabilidade:
- Distribuição Binomial;
- Distribuição de Poisson;
- Distribuição Normal; e,
- Distribuição Exponencial.
Selecione a alternativa que contém, dentre as distribuições listadas, as que pertencem à Família Exponencial.
Um componente tem a vida útil (em horas) regida pela distribuição exponencial com média θ horas. Qual a probabilidade de um dado componente atender à demanda de θ horas?
Com o objetivo de se estimar a média desconhecida de uma população normalmente distribuída, foi selecionada uma amostra de tamanho 90. A um nível de significância de 5%, a estimativa intervalar gerou um erro de 2. Quantos elementos a mais deveriam ser incorporados à amostra, se desejássemos reduzir o erro para 1,5 em torno do valor da média, mantendo-se o mesmo nível de significância?
Em uma cidade foi realizada uma pesquisa entre 600 eleitores, escolhidos aleatoriamente, com relação à preferência entre 2 candidatos X e Y para o cargo de prefeito. Esta pesquisa forneceu 2 grupos de eleitores, sendo 375 homens e 225 mulheres. Cada eleitor forneceu uma e somente uma resposta, na pesquisa, se preferia X ou Y.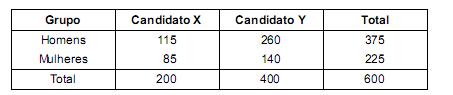
O objetivo é verificar, com relação a estes eleitores, se a preferência pelos candidatos depende do sexo, utilizando o teste qui- quadrado a um determinado nível de significância a.
Dados:
Valores críticos da distribuição qui-quadrado [P(qui-quadrado com n graus de liberdade) < valor tabelado = 95%] 
É correto afirmar que
Atenção: Para resolver às questões de números 38 a 40, use, dentre as informações dadas a seguir, as que julgar apropriadas.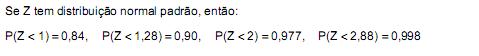 
O volume líquido de frascos de xampu é uma variável aleatória com distribuição aproximadamente normal com média µ e desvio padrão 0,5 mL. O valor de µ, em mL, para que no máximo 0,2% dos frascos tenham menos do que 200 mL é
Para n = 250 e q = 1,5%, sendo q a probabilidade de sucesso, a média da distribuição de Poisson (µ) é
Durante 36 dias, observou-se, diariamente, a quantidade produzida de peças por duas máquinas de marcas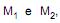 
independentemente. Um fabricante verificou que subtraindo diariamente da quantidade de peças produzidas por 
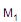a quantidade produzida por 
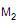obteve a presença de sinal positivo nas diferenças de 20 produções e sinal negativo nas 16 restantes, não ocorrendo diferença nula. Aplicando o teste dos sinais para decidir se a proporção populacional de sinais positivos (p) é igual a 0,50, ao nível de significância de 5%, ele considerou as hipóteses 
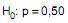(hipótese nula) contra 
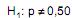(hipótese alternativa). Com a aproximação da distribuição binomial pela normal sem a correção de continuidade, foi apurado o valor do escore r correspondente para comparação com o valor crítico da distribuição normal padrão (Z) tal que a probabilidade 
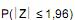= 95%. Então, o fabricante, ao nível de significância de 5%,
Dada uma distribuição binomial com n = 10 e 40% de probabilidade de ocorrência de um evento, a variância é
