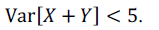Analise as afirmativas abaixo, referentes à geração de números aleatórios:
I. Os números gerados por um computador como aleatórios são considerados pseudoaleatórios, uma vez que existe um algoritmo que origina esses números.
II. Caso o algoritmo gere em algum momento o número usado como semente, a sequência de números pseudoaleatórios deverá se repetir.
III. O número que inicia o algoritmo de geração de números pseudoaleatórios é conhecido como semente.
Quais afirmativas estão corretas:
Definida (o) por um vetor de médias e a matriz de variância-covariância. É uma extensão da distribuição normal univariada para aplicações com um grupo de variáveis que podem ser correlacionadas. Refere-se a:
Um fabricante de carros elétricos concede garantia da bateria por 10 anos. Decorrido esse prazo, dos 10 mil carros vendidos, nenhum carro apresentou defeito na bateria.
A conclusão a que se pode chegar com base na ciência estatística é:
Quais os métodos abaixo são de estimação por métodos computacionais:
Seja uma população regida por uma distribuição de probabilidade com média θ e variância 25. A fim de se estimar o valor do parâmetro θ, propôs-se o estimador T(X1, X2) = aX1 + βX2 a partir de uma amostra de tamanho 2, de tal forma que o estimador assim definido seja não tendencioso e tenha variância 13, com α > 0 e β > 0 . Qual o valor de α x β ?
Uma distribuição de probabilidades é usada para determinar a média de uma população, a partir de uma amostra. Nesse problema, não se sabe qual é a média ou o desvio padrão da população, mas ela deve ser normal. Considere que o tamanho da amostra é igual a nove, e se deseja testar uma hipótese com 5% de significância. Dois estatísticos utilizam duas distribuições diferentes. O estatístico Tiago utiliza a distribuição t de Student e o estatístico Nelson utiliza a distribuição normal.
Se o valor da estatística teste obtido é exatamente igual a 2 para o problema analisado, é correto afirmar que ao testar a hipótese estatística:

Qual das alternativas abaixo pode ser considerado um processo de Markov em tempo contínuo?
A Distribuição de Poisson fornece a probabilidade de vários eventos ocorrerem em um intervalo fixo de tempo ou espaço. Onde esses eventos acontecem com uma taxa média conhecida e independentemente do tempo desde o último evento. De acordo com a distribuição de Poisson análise o caso seguinte: José Marcos, funcionário da Agência bancária Beta, em Guarapari, atende 5 clientes em 10 minutos.
Fórmula:
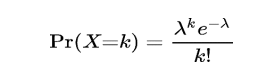
Onde:
(λ) = Lâmbda – número real que corresponde ao número de ocorrências que se espera dentro de um determinado intervalo de tempo.
Pr = tende ao valor;
x = é uma variável aleatória que terá o valor k;
k = número inteiro que não pode ser negativo, pois corresponde a quantidade de vezes que, dentro de certo intervalo, um evento ocorre;
e = trata-se do número de Euler que é irracional e cujo valor aproximado é 2,71828.
Utilizando a distribuição de Poisson, qual é a probabilidade de José Marcos atender 8 clientes em um intervalo de 10 minutos?
Na prática, os experimentos realizados permitem somente dois resultados. Ex: cara ou coroa, negativo ou positivo, sim ou não, aprovado ou reprovado, etc. Há na estatística diversas distribuições especiais. As características a seguir, são referentes a qual distribuição especial da estatística?
• O número de tentativas é fixo (n);
• As n tentativas são independentes e repetidas em condiçõesidênticas;
• Para cada tentativa há dois resultados possíveis: s=sucesso ou f=fracasso;
• A probabilidade de sucesso numa tentativa única é p. P(S) = p.
• A probabilidade de fracasso é q. P(F)=q, onde p+q= 1
• O problema central está em determinar a probabilidade de x sucessos e n tentativas, sendo x=0 ou 1 ou2...n.
• A variável aleatória x é uma contagem do número de sucessos em n tentativas.
• Repetições independentes de um ensaio de Bernoulli, com a mesma probabilidade de ocorrência de “sucesso”, dão origem a essa distribuição.
Qual é a distribuição a seguir?
Após a cerimônia de posse dos novos servidores aprovados em um concurso para o TJDFT, os recém-nomeados precisam realizar um curso de capacitação especializado.
Ao final do curso, os alunos avaliam o curso de forma negativa, se suas expectativas não tiverem sido atendidas, ou de forma positiva, caso contrário.
Os dados estão representados na tabela a seguir.
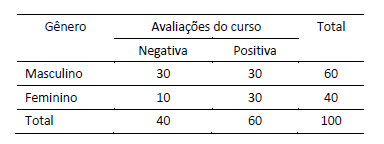
Com o objetivo de concluir se as avaliações são ou não dependentes do gênero, realizou-se o teste do qui-quadrado.
O valor do χ2 observado foi de 6,25.
Utilizando-se um nível de 10% de confiança, é possível concluir que:
Considerando os modelos e as hipóteses relacionadas ao cálculo do valor em risco (VAR – value at risk), julgue o próximo item.
Se os dados utilizados para o cálculo do VAR seguem uma distribuição normal, então será evidenciada a propriedade matemática de subaditividade
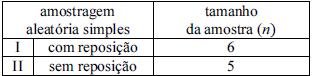
Suponha que determinada população de tamanho N = 100 seja constituída pelos elementos x1, ..., x100. Para a realização de um levantamento amostral sobre essa população, cogitam-se duas possibilidades mostradas no quadro anterior, ambas pelo método de amostragem aleatória simples. Se o tipo I for o escolhido, então a amostragem será com reposição com n = 6. No entanto, se o escolhido for o tipo II, então a amostra será sem reposição com n = 5.
Com base nessas informações, julgue o item que se segue.
Na amostragem do tipo I, a probabilidade de que o elemento da população x20 constitua a amostra de tamanho n = 6 é igual a 0,09.
A média e a variância de uma distribuição binomial são, respectivamente, 20 e 4. O número de ensaios (n) dessa distribuição é: