Um paralelepípedo com 3 (três) centímetros de base, 5 (cinco) centímetros de altura e 6 (seis) centímetros de profundidade, possui quantos centímetros quadrados de área da sua superfície:
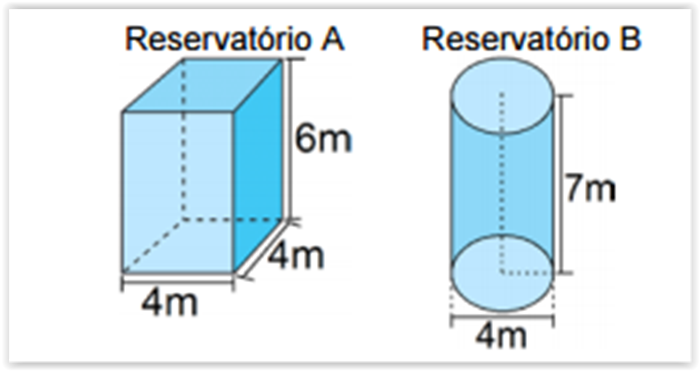
Considerando-se as dimensões dos reservatórios A e
B apresentadas na imagem abaixo e a capacidade
máxima de armazenamento de cada reservatório,
assinalar a alternativa CORRETA:
(Usar: π = 3,14 )
Para acondicionar um novo produto, uma fábrica encomendou uma embalagem com medidas 15 cm de comprimento, 30 cm de largura e 5 cm de altura. O mesmo produto será feito em embalagem promocional tamanho família, que tem que ter o dobro do volume da embalagem original. As dimensões da embalagem que respeitam essa condição para essa embalagem promocional (ter o dobro do volume da original) é
Uma piscina com 25 (vinte e cinco) metros de comprimento, 10 (dez) metros de largura e 5 (cinco) metros de profundidade está preenchida com água com capacidade equivalente a 7/8 de sua capacidade total. Qual é o volume de água, em litros, pressente nesta piscina?
Uma pirâmide reta de base quadrada está inscrita em um cilindro cuja base tem 18πcm2 e de volume igual a 216πcm3 . Qual é o volume dessa pirâmide?
Para um cone reto com g = 10 cm e r = 8 cm, encontre o volume.
Uma lagartixa está no interior de um quarto e começa a se deslocar. Esse quarto, apresentando o formato de um paralelepípedo retangular, é representado pela figura.
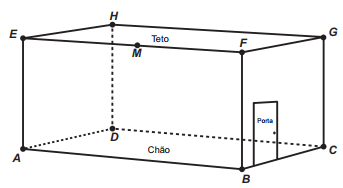
A lagartixa parte do ponto B e vai até o ponto A. A seguir, de A ela se desloca, pela parede, até o ponto M, que é o ponto médio do segmento EF. Finalmente, pelo teto, ela vai do ponto M até o ponto H. Considere que todos esses deslocamentos foram feitos pelo caminho de menor distância entre os respectivos pontos envolvidos.
A projeção ortogonal desses deslocamentos no plano que contém o chão do quarto é dado por:
Um prédio instalou uma caixa d’água no formato de cubo com 3 metros de altura, 5 metros de comprimento e 2 metros de profundidade. Desta forma, podemos dizer que a capacidade da caixa d’água é:
Uma construtora solicita ao seu fabricante de pré-moldados que altere as dimensões dos blocos retangulares utilizados na construção de paredes. Foi solicitado que cada bloco tenha comprimento externo de 100 cm e largura externa de 15 cm. O fabricante calculou que a espessura da parede do bloco será de 3 cm para suportar o peso no empilhamento dos blocos, sendo necessário dimensionar a altura do bloco de forma a utilizar um volume de concreto de 39 240 cm3 na produção de cada bloco, conforme ilustra a figura.
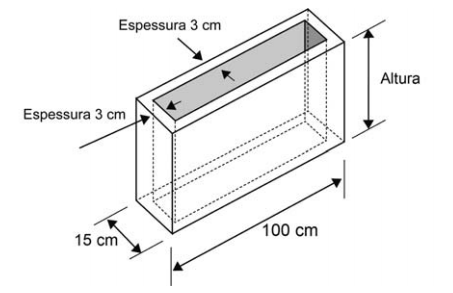
Nessas circunstâncias, qual deve ser a altura do bloco, em centímetro?
Uma pessoa ganhou uma pulseira formada por pérolas esféricas, na qual faltava uma das pérolas. A figura indica a posição em que estaria faltando esta pérola.

Ela levou a joia a um joalheiro que verificou que a medida do diâmetro dessas pérolas era 4 milímetro. Em seu estoque, as pérolas do mesmo tipo e formato, disponíveis para reposição, tinham diâmetro iguais a : 4,025 mm; 4,100 mm ; 3,970 mm ; 4,080 mm e 3,099 mm.
O joalheiro então colocou na pulseira a pérola cujo diâmetro era o mais próximo do diâmetro das pérolas originais.
A pérola colocada na pulseira pelo joalheiro tem diâmetro, em milímetro, igual a
O volume de um cubo é de 343 metros cúbicos. Qual é a medida de cada lado deste cubo?
Uma laje maciça está pronta para a concretagem. O técnico responsável pela obra está encomendando o concreto, que deverá ser bombeado. Sabe-se que a laje possui 15 cm de espessura, 4,50 m de largura e comprimento igual a 20,50 m, portanto, o volume mínimo de concreto a ser encomendado é, em m3 , igual a
Considere um prisma triangular reto e regular cujo lado da base mede 2 cm. Assuma ainda que esse prisma possui altura medindo 6 cm. Qual o volume desse prisma?
Considere dois cones retos, o cone A tem raio r1 e cone B tem raio r2 . Sabendo que a altura do cone B é o dobro do cone A e que o volume do come A é um terço do volume do B, qual a relação entre os raios dos dois cones?
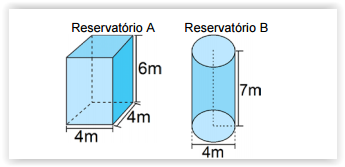
Considerando-se as dimensões dos reservatórios A e
B apresentadas na imagem abaixo e a capacidade
máxima de armazenamento de cada reservatório,
assinalar a alternativa CORRETA:
(Usar: π = 3,14 )