Dados os planos x + 2y – 2z + 1 =0 e 2x + 4y - 4z + 4 = 0, calcule a distância entre eles para um ponto (1,1,2) situado no primeiro plano.
Dados os pontos A(2; 3) e B(0; –2). A equação da reta que passa pelos pontos A e B é:
O número máximo possível de pontos de interseção entre uma reta e uma cônica é
Sendo a linha L1 uma circunferência cujo centro é o ponto P(u,v), então, a soma u + v é igual a
A distância entre a linha L2 e a reta representada pela equação 3x + 4y = 0, em u.c., é
Um triângulo retângulo tem seus vértices nos pontos de coordenadas cartesianas (0 , 0) , (3 , 0) e (0 , 4). O perímetro deste triângulo mede:
A respeito dos números complexos, julgue o item a seguir.
As raízes do polinômio z3 - 3z2 + 3z = 0, no plano complexo, são vértices de um triângulo inscrito no círculo de centro no ponto (1, 0) e de raio 1, isto é, se z = x + iy for uma dessas raízes, então (x - 1)2 + y2 = 1.
Das alternativas, qual indica a distância entre os pontos A e B, sendo as coordenadas de A = (2, 5) e as coordenadas de B = (7, 5)?

As coordenadas que correspondem ao ponto indicado no mapa são
Dados os pontos A(2,2) e B(4,4), qual a distância entre eles?
Se M(6,8) é ponto médio do segmento LN, em que L(2,3) e N(x,y) representam as extremidades desse segmento, podemos afirmar que y-x vale
Uma logomarca é formada por quatro semicircunferências, duas a duas concêntricas: c1 e c3, c2 e c4. As semicircunferências c1 e c2 têm raio R. A distância entre as semicircunferências concêntricas mede d.

Considere que o comprimento da semicircunferência
c1 é 
A medida da área da região sombreada, em m2, é
Se a interseção da linha L2 e a reta representada pela equação 3x + 2y – 6 = 0 é o ponto H(s, t), então, o resultado numérico da expressão s2 + t2 é
A figura seguinte mostra, em um sistema de coordenadas cartesianas ortogonais xOy, em que a unidade de medida é o metro, uma região retangular OABC. O lado OA mede 600 m e o lado OC mede 800 m.
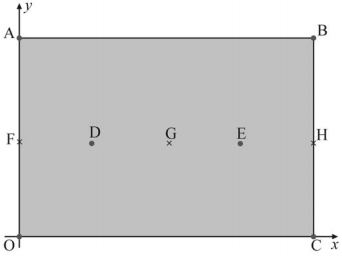
A figura mostra também os pontos F = ponto médio de OA, H = ponto médio de CB, G = centro do retângulo OABC, D = ponto médio de FG, e E = ponto médio de GH. Nos pontos O, A, B, C, D e E foram instalados pontos de acesso à Internet — wi-fi. Nessa configuração, o usuário consegue se conectar à Internet desde que o seu smartphone esteja a 200 m ou menos de qualquer desses pontos de acesso.
Com base nessas informações e na figura apresentada, julgue o próximo item.
Se um smartphone está em um drone, a 50 m de altura sobre o ponto P = (100, 100), então, nesse caso, é possível conectá-lo à Internet a partir do ponto de acesso localizado na origem O.
O centro da circunferência λ: x2 + y2 -2x -4y = 4 é o foco de uma parábola cuja diretriz é o eixo Ox do plano cartesiano.
A equação dessa parábola é


