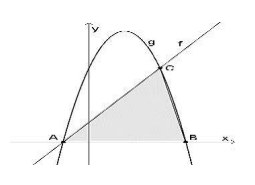
A figura a seguir apresenta os gráficos de duas funções f e g, afim e quadrática, respectivamente. Os vértices do triângulo ABC pertencem ao gráfico da função g(x) = -2x2 + 4x + 4. Sabendo que a área desse triângulo é 4√3 unidades quadráticas, o coeficiente angular da função f é:
Considere o triângulo ABC com vértices A = (- 6, - 2), B = ( 6, 1) e C = ( 2, 4). Prolonga-se os segmento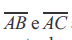 
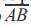
a partir dos pontos B e C, respectivamente. Em seguida trace uma bissetriz exterior a partir do ponto C até interceptar o prolongamento do segmento 
no ponto Q.Determine a área do triângulo ACQ, a qual vamos denotar por S, sabendo que as medidas são dadas em metros e indique o resultado
CORRETO:
Considere a parábola definida por y = x2 – 4x +7 e a circunferência definida por (x -2)2 + (y -3)2 = 4. Assinale a alternativa que indica em quantos pontos estas duas curvas se interceptam.
Se r: 4x - 3y + 15 = O é uma reta contida no plano R² calcule a distância entre r e o ponto P (1 , -2).
Os lados de um triangulo ABC estão contidos nas retas r: 4x + 2y + 3 = 0, s: 2x + 4y – 27 = 0 e t: 4x – 2y – 11 = 0. A área da circunferência inscrita nesse triângulo, em unidades quadradas, é:
GeoGebra é um aplicativo gratuito para descrever gráficos através da digitação da equação de uma curva. Ana utilizou esse aplicativo para descrever a equação da reta r: y = 3x -2. Em seguida digitou a equação da reta s paralela à reta r. Dentre as retas descritas a seguir a equação da reta s digitada por Ana pode ser:
As retas de equações y + x – 4 = 0 e 2y = 2x – 6 são, entre si,
Em um sistema de coordenadas cartesianas ortogonais xOy,
o conjunto dos pares (x, y) que satisfazem uma equação da
forma Ax2 + By2 + Cxy + Dx + Ey + F = 0, em que A, B, C, D, E e
F são constantes reais, pode representar: um único ponto;
uma reta; duas retas; uma circunferência; uma elipse; uma
hipérbole; uma parábola; ou um conjunto vazio. A respeito
desse assunto, julgue os itens seguintes.
A equação x2 + y2 – 4x + 6y + 12 = 0 representa umacircunferência de centro no ponto (2, -3) e raio 1
Considere as duas equações de retas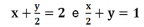 
. Assinale a alternativa correta acerca da relação entre estas duas retas.
Considere a equação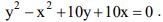
Esta equação corresponde a
Uma circunferência dada por x² + y² - 200 = 0 tem uma reta tangente e paralela à reta y = x – 10 dada pela equação
Um triângulo com vértices (5,0), (10,0) e (0,10) gira em torno do eixo das ordenadas, determinando um sólido com volume igual a
O ponto médio de um segmento de reta com extremos P 1(x1,y1) e P2(x2,y2) é dado pela fórmula do ponto médio. Com base nisso, assinale a alternativa correta.
Um menino acaba de se mudar para um novo bairro e deseja ir à padaria. Pediu ajuda a um amigo que lhe forneceu um mapa com pontos numerados, que representam cinco locais de interesse, entre os quais está a padaria. Além disso, o amigo passou as seguintes instruções: a partir do ponto em que você se encontra, representado pela letra X, ande para oeste, vire à direita na primeira rua que encontrar, siga em frente e vire à esquerda na próxima rua. A padaria estará logo a seguir.
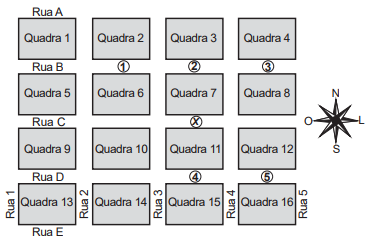
A padaria está representada pelo ponto numerado com
Seja a equação geral da reta ax + by + c = 0. Quando a = 0, b ≠ 0 e c ≠ 0, a reta
