Considere os conjuntos P e Q dados por:
P = {1, 2, 8, 9, 15, 11} e Q = {1, 3, 6, 8, 7, 14, 33, 9}
Qual das alternativas apresenta o conjunto P n Q?
Considerem-se verdadeiras as seguintes afirmações:
“Todo rubro-negro é feliz.”
“Alguns pernambucanos são rubro-negros.”
“Alguns pernambucanos são alvirrubros.”
“Nenhum rubro-negro é alvirrubro.”
Qual das seguintes afirmações é verdadeira?
Uma editora estuda a possibilidade de relançar duas obras
da literatura: Iracema e A Moreninha. Para isso, efetuou
uma pesquisa de mercado e concluiu que, em cada 1.000
pessoas consultadas:
- 600 leram Iracema;
- 400 leram A Moreninha;
- 120 leram as duas obras.
Considerando essas afirmações, é correto afirmar que o
número de pessoas que leram apenas uma das duas obras
foi de:
Considere como verdadeiras as afirmações: - Todo programador sabe inglês. - Todo programador conhece informática. - Alguns programadores não são organizados. A partir dessas afirmações é correto concluir que
Considere o conjunto A formado por todos os números inteiros
positivos, não nulos, menores que 40 e pares. Além disso,
considere também um conjunto B formado por todos os
números inteiros positivos, não nulos, menores que 40 e
divisíveis por três. Assinale a seguir a alternativa que
apresenta a quantidade de elementos contidos no conjunto C,
formado pela intersecção dos conjuntos A e B.
Observando uma caixa com
objetos de plástico, fez-se as seguintes
afirmações:
Nem todos os objetos da caixa são
vermelhos. Nenhum objeto da caixa é
redondo. Supondo que as afirmações são verdadeiras,
então é correto deduzir que é verdadeiro:
Em uma empresa foram apresentados dois projetos A e B para avaliação. A fim de qualificar os projetos, 20 (vinte) funcionários da empresa avaliaram cada um dos projetos com um dos seguintes conceitos: aprovado ou reprovado. Sabendo que 3 (três) funcionários não aprovaram nenhum dos projetos, 15 (quinze) funcionários aprovaram o projeto A e 10 (dez) funcionários aprovaram o projeto B, é correto afirmar que o número de funcionários que aprovaram ambos os projetos é igual a:
Passeando na vila, Alberto encontrou três habitantes e sabia que apenas um deles era médico, mas não sabia qual. Esses três habitantes, identificados por A, B e C, fizeram as seguintes afirmações: A: “Olá, eu sou o médico da vila.” B: “Olá, eu não sou o médico da vila.” C: “Olá, no máximo um de nós sempre fala a verdade.” A partir dessas afirmações, Alberto concluiu corretamente que o médico pode ser
Determinada faculdade oferta, em todo semestre, três
disciplinas optativas para alunos do quinto semestre: Inovação e
Tecnologia (INT); Matemática Aplicada (MAP); Economia do
Mercado Empresarial (EME). Neste semestre, dos 150 alunos que
possuíam os requisitos necessários para cursar essas disciplinas,
foram registradas matrículas de alunos nas seguintes quantidades:
• 70 em INT;
• 45 em MAP;
• 60 em EME;
• 25 em INT e MAP;
• 35 em INT e EME;
• 30 em MAP e EME;
• 15 nas três disciplinas.
Com base nessas informações, julgue os itens que se seguem.
Os dados disponíveis são insuficientes para se determinar a quantidade de alunos que não efetuaram matrícula em nenhuma das três disciplinas.
Uma orquestra possui músicos que tocam instrumentos de sopro, corda e percussão. Dez músicos tocam instrumentos de sopro e de corda, oito tocam instrumentos de corda e percussão e cinco tocam instrumentos de sopro e percussão. Sabe-se, ainda, que dois músicos tocam os três tipos de instrumentos. Quantos músicos tocam mais de um instrumento?
Considere o diagrama na
imagem abaixo:
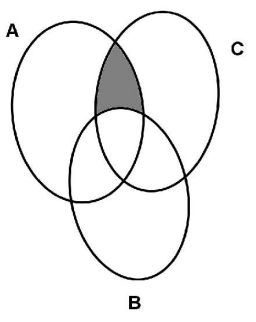
De acordo com esse diagrama:
A representa o conjunto dos objetos vermelhos. B representa o conjunto dos objetos na forma
de quadrado. C representa o conjunto dos objetos de tamanho
pequeno. Então, a região sombreada na imagem
representa os objetos que possuem as
características de:
Em uma empresa de porte médio, 217 funcionários têm casa própria ou carro ou as duas coisas. Se 189 têm carro e 63 têm casa própria, o número de funcionários que têm carro mas não têm casa própria é:
Uma avaliação com apenas duas questões foi respondida
por um grupo composto por X pessoas.
Sabendo–se que exatamente 160 pessoas desse
grupo acertaram a primeira questão, que exatamente
100 pessoas acertaram as duas questões, que exatamente
250 pessoas acertaram apenas uma das duas
questões, e que exatamente 180 pessoas erraram a
segunda questão, é possível afirmar, corretamente,
que X é igual a
Sabe-se que todos os primos de Vanderlei são funcionários públicos e que todos os primos de Marcelo não são funcionários públicos. Dessa forma, deduz-se corretamente que
Em uma empresa trabalham homens e mulheres sendo, ao todo, 80 pessoas. Dentre elas, sabe-se que:
· 20 falam inglês;
· 45 são homens;
· 26 mulheres não falam inglês.
O número de homens que trabalham nessa empresa e não falam inglês é:

