Após o processo de recuperação de uma reserva ambiental, uma espécie de aves, que havia sido extinta nessa reserva, foi reintroduzida. Os biólogos responsáveis por essa área estimam que o número P de aves dessa espécie, t anos após ser reintroduzida na reserva, possa ser calculado pela expressão
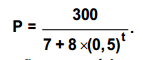
De acordo com essa estimativa, quantos anos serão necessários para dobrar a população inicialmente reintroduzida?
Considere a equação polinomial x3 + x2 + kx = 0 , onde k é um coeficiente real.
Se uma das raízes dessa equação é 4, as outras raízes são
Dentro de uma gaveta há garfos, facas e colheres, totalizando 48 talheres. A soma das quantidades de garfos e de facas corresponde ao dobro da quantidade de colheres. Se fossem colocadas mais 6 facas dentro dessa gaveta, e nenhuma colher fosse retirada, a quantidade de facas se igualaria à de colheres.
Quantos garfos há nessa gaveta?
Em certo ano bissexto (com 366 dias), o dia 1º de janeiro caiu em um domingo. Nesse ano, Antônio, no dia do seu aniversário, disse para sua família no jantar: “No dia de hoje, completamos a terça parte deste ano”. O dia do aniversário de Antônio nesse ano foi:
Sete bolas brancas e sete bolas pretas foram distribuídas em quatro caixas, e a figura abaixo mostra quantas bolas cada caixa contém.
Sabe-se que:
- cada caixa contém, pelo menos uma bola branca;
- a terceira caixa contém quantidades iguais de bolas brancas e pretas;
- a quarta caixa possui mais bolas brancas do que pretas.
Retirando ao acaso uma bola de cada caixa, a probabilidade de que todas sejam brancas é:
Um consumidor comprou 3 caixas de leite em um supermercado e pagou o total de R$ 8,34. Determine quanto pagaria se comprasse 7 caixas do mesmo leite nesse supermercado.
Mario fez uma viagem de ônibus que durou três horas e meia. Assim que o ônibus partiu, Mario dormiu. Quando acordou, dois quintos do tempo da viagem haviam passado.
O tempo que Mario passou dormindo nessa viagem foi de:
Uma senha de 5 caracteres distintos deve ser formada usando as letras A e O e os números 0, 1, 2. As senhas devem começar e terminar com letras, mas não é permitido usar o 0 (zero) ao lado do O (letra o).
Quantas senhas podem-se formar atendendo às regras estabelecidas?
Partindo do ponto A, um automóvel percorreu 4,5 km no sentido Leste; percorreu 2,7 km no sentido Sul; percorreu 7,1 km no sentido Leste; percorreu 3,4 km no sentido Norte; percorreu 8,7 km no sentido Oeste; percorreu 4,8 km no sentido Norte; percorreu 5,4 km no sentido Oeste; percorreu 7,2 km no sentido Sul, percorreu 0,7 km no sentido Leste; percorreu 5,9 km no sentido Sul; percorreu 1,8 km no sentido Leste e parou. A distância entre o ponto em que o automóvel parou e o ponto A, inicial, é igual a
Uma empresa de construção civil tem 8 pedreiros no seu quadro de empregados que recebem, atualmente, R$ 1.500,00 de salário base, R$ 350,00 de auxílio alimentação e R$ 150,00 de auxílio transporte. O salário bruto de cada um deles corresponde à soma desses três valores e, a partir do próximo mês, o salário base e o auxílio alimentação desses empregados serão reajustados em 15%.
Diante da situação apresentada acima e considerando que o total dos descontos legais com previdência e imposto de renda corresponda a 30% do salário bruto e que todos os pedreiros da construção civil trabalhem com a mesma eficiência, julgue o seguinte item.
Considere que a empresa tenha capacidade de construir, com seus 8 pedreiros, 400 m2 de paredes em 21 horas de serviço. Considere, ainda, que haja necessidade de aumentar a capacidade para 500 m2 em 14 horas e que isso só seja possível com a contratação de mais pedreiros, cujos salários brutos serão pagos com a quantia de R$ 15.000,00, total disponível para a empresa. Nesse caso, a empresa não terá condições de arcar com a folha de pagamentos após o reajuste salarial previsto para o próximo mês.
Em uma sala estão 60 candidatos de um concurso público, aguardando a distribuição do caderno de questões da prova. Dos 60 candidatos, 24 usam óculos, 33 usam óculos ou são canhotos e, 48 são destros. Um candidato será escolhido ao acaso para verificar que o pacote contendo as provas está lacrado. Considerando que nenhum dos 60 candidatos é ambidestro, determine a probabilidade de ser escolhido um candidato que use óculos e seja canhoto.
Em uma agência bancária, os clientes são atendidos da seguinte maneira: todos os clientes a serem atendidos em determinado dia comparecem à agência no período compreendido entre 10 horas da manhã e meio-dia; ao chegar à agência, o cliente recebe uma senha para o posterior atendimento, que corresponde à sua ordem de chegada, ou seja, o primeiro cliente a chegar à agência recebe a senha 1, o segundo recebe a senha 2, e assim por diante; ao meio-dia, quando é encerrada a distribuição de senhas, os clientes que as receberam começam a ser atendidos, na ordem estabelecida por elas, ou seja, na ordem de chegada do cliente à agência no horário entre 10 horas e meio-dia. Depois que o atendimento efetivamente começa, o tempo quem um cliente espera para ser atendido é diretamente proporcional ao número de clientes que chegaram antes dele e inversamente proporcional ao número de atendentes.
Durante o mês de janeiro de 2014, essa agência trabalhou diariamente com um quadro de 10 atendentes, que levavam exatos 15 minutos para atender 25 clientes. No dia 30/1/2014, 200 clientes foram atendidos nessa agência, ao passo que, no dia 31/01/2014, esse número subiu para 800 clientes. Preocupado com essa situação e prevendo que a quantidade de clientes que procurariam a agência no dia 3/02/2014 seria ainda maior, o gerente decidiu que, durante o mês de fevereiro, o número de atendentes cresceria em 20% em relação ao número de atendentes de janeiro, assegurando que o nível de eficiência dos novos atendentes fosse idêntico ao nível dos que já estavam atuando. Sua decisão foi implementada já em 3/2/2014.
Com base nas informações acima, julgue os itens seguintes.
No dia 30/01/2014, o 61º cliente que compareceu à agência foi atendido depois das 12h35min.
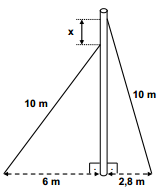
Um mastro é mantido na vertical por meio de dois cabos de 10 m de comprimento. O primeiro está fixado a 6 m da base do mastro, e o segundo a 2,8 m da base, conforme indica a figura. Determine a distância x entre as alturas dos pontos de fixação dos cabos no mastro.
Considere as informações a seguir para responder às
questões de n
os 59 e 60.
O Modelo Digital de Elevação de uma grande bacia hidrográfica
rural tem resolução espacial de 100 metros e
pode ser representado pela matriz a seguir. Para cada
elemento da célula, indica-se a elevação representativa
em metros e, assim, pode-se estabelecer a direção preferencial
de escoamento, considerando que a água vá fluir
de uma célula para a outra segundo o critério de maior
declividade.
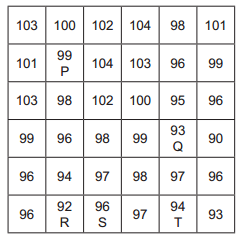
Pretende-se escavar um canal que leve o escoamento que chega à célula de cota 95 metros até a célula indicada pela letra R. Caso a intervenção seja realizada, a área de drenagem da célula indicada pela letra R aumentaria de um valor entre
Para o conjunto Ω = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, se A for um subconjunto de Ω, indique por S(A) a soma dos elementos de A e considere S(∅) = 0. Nesse sentido, julgue os itens a seguir.
É possível encontrar conjuntos A e B, subconjuntos de Ω, disjuntos, tais que A∪B = Ω e S(A) = S(B).

