Um tanque com a forma de um paralelepípedo retângulo de dimensões 300 cm, 4 m e 20 dm está com 3/4 do volume ocupados com água. Sabendo que 1 dm3 = 1 litro, quantos litros de água faltam para encher completamente o tanque?
Jonas está montando um castelo de cartas de modo que cada nível do castelo possui 3 vezes o número de cartas do
nível superior. Assim, o nível mais alto do castelo possui 2 cartas, o nível imediatamente abaixo possui 6 cartas e,
assim, sucessivamente. Sabendo que o castelo possui um total de 2.186 cartas, então o número de níveis desse
castelo é:
Observa a sequência numérica e assinale a alternativa que representa o próximo número da sequência 106 ; 99 ; 81 ; 72 ; ...
Os números 3 ;4 e 5 são conhecidos como trio Pitagórico pois 32+42=52. Qual das alternativas seguintes também representa um trio Pitagórico?
Uma determinada espécie de peixe fornece sessenta por cento de carne em relação ao seu peso total, se Juliana pescou doze peixes desta espécie totalizando nove quilos e oitocentas gramas. Qual a quantidade de carne que ela vai levar pra casa após os peixes serem limpos?
Leia o texto abaixo e responda:
Missão Possível
Durante a adolescência Fabiana Murer era uma das melhores ginastas de Campinas, no
interior de São Paulo, e sonhava em participar de uma olimpíada. Aos 16 anos, já muito
alta para a ginástica artística (hoje, aos 27 anos, ela mede 1,72 metro), decidiu tentar a
sorte no atletismo. O treinador Edson Miranda, que a acompanha até hoje, apostou que ela
poderia se dar bem no salto de vara. Ele não estava errado. Além de vencer o Pan do Rio,
no ano passado, Fabiana superou em 20 centímetros o recorde da competição ao saltar 4,6
metros. Em junho, no troféu Brasil de Atletismo, alcançou 4,8 metros, conquistou a
medalha de ouro e quebrou o recorde sul-americano. Para Pequim, ela já estabeleceu sua
meta. “Vai ser difícil conquistar uma medalha, mas não impossível", diz. (In: Veja,
20/02/2011)
Sistema Métrico Decimal:
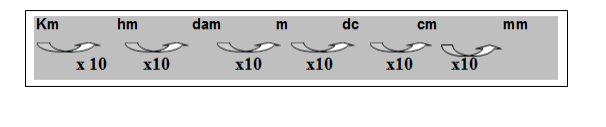
Sabendo que um centímetro é a centésima parte de um metro. Qual o número
fracionário que representa a superação do recorde da competição no Pan do Rio, em
metros?
Suponha que, de um baralho normal, contendo 52 cartas de quatro naipes, é extraído, sem reposição e aleatoriamente, um total de quatro cartas. Se a carta “Ás” é equivalente a uma figura (ou seja, são 4 figuras e 9 números de cada naipe), é correto afirmar que a probabilidade de que todas sejam:
Suponha que, de um baralho normal, contendo 52 cartas de quatro naipes, é extraído, sem reposição e aleatoriamente, um total de quatro cartas. Se a carta “Ás” é equivalente a uma figura (ou seja, são 4 figuras e 9 números de cada naipe), é correto afirmar que a probabilidade de que todas sejam:
Seja (2, 25) ponto pertencente ao gráfico da função exponencial
Sabe-se que 6 máquinas iguais, trabalhando ininterruptamente durante 6 horas por dia, produzem n unidades de certa peça em 6 dias. Se as mesmas 6 máquinas trabalharem ininterruptamente durante 8 horas por dia, o número de dias necessários para a produção de n unidades da mesma peça será reduzido em
Certa escola tem 15 classes no período matutino e rascunho 10 classes no período vespertino. O número médio de alunos por classe no período matutino é 20, e, no período vespertino, é 25. Considerando os dois períodos citados, a média aritmética do número de alunos por classe é
Sendo P e Q dois conjuntos não vazios, de modo que P ⊂ Q. Em relação assinale a afirmação verdadeira.
Todas as Progressões Geométricas abaixo estão classificadas corretamente, EXCETO.
O gráfico que representa a
função: f(x) = - x + 4 é:
Calculando 20 - (10 + √20¡ ) + 5 + (7 + √45¡ ) o
resultado é:

