Em uma instituição de ensino, a nota final de cada aluno RAS C U NHO é calculada pela média aritmética ponderada das notas dos quatro bimestres, com pesos 1, 2, 3 e 4, para os bimestres de 1 a 4, respectivamente. Para ser aprovado, o aluno tem que atingir nota final 5. Sendo assim, um aluno que tirou no primeiro, segundo e terceiro bimestres notas 4, 6 e 3, respectivamente, precisa tirar, no quarto bimestre para ser aprovado, no mínimo, uma nota igual a
Uma chácara em formato retangular, com perímetro de
3400 metros, tem um dos lados medindo 700 metros
mais que o outro. Logo, a área dessa chácara, em metros
quadrados, é
Três números somados totalizam 180. Sabendo que eles são proporcionais aos números 4, 5 e 6. Quais seriam estes números?
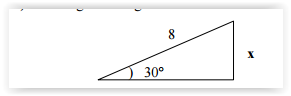
No triângulo retângulo o valor de x é:
Calcule o juro simples e o montante de um investimento de R$ 340,00 à taxa de 7% ao ano pelo prazo de 3 anos. Onde a alternativa correta é:
Pretende-se dividir um grupo de 216 pessoas, sendo 126 com formação na área de exatas e 90 com formação na área de humanas, em grupos menores contendo, obrigatoriamente, elementos de cada uma dessas áreas, de modo que: (1) o número de grupos seja o maior possível; (2) cada grupo tenha o mesmo número x de pessoas com formação na área de exatas e o mesmo número y de pessoas com formação na área de humanas; e (3) cada uma das 216 pessoas participe de um único grupo. Nessas condições, e sabendo-se que no grupo não há pessoa com ambas as formações, é correto afirmar que, em cada novo grupo, a diferença entre os números de pessoas com formação em exatas e em humanas, nessa ordem, será igual a
Uma pessoa comprou um determinado produto cujo preço à vista era de R$ 825,00. Como forma de pagamento, ela deu uma entrada de 45% do preço à vista e pagou o restante com um cheque para 30 dias, com juros de 4% sobre esse restante. O valor que essa pessoa pagou de juros, nessa compra, correspondeu a
Todos os dias, são necessárias, em média, duas horas
para cinco analistas, todos com a mesma força de trabalho,
analisarem determinada quantidade Q de documentos.
Em um dia em que um desses analistas não puder
realizar essa tarefa, espera-se que os quatro demais, no
mesmo ritmo de trabalho, realizem metade dessa tarefa
em, no mínimo, 1 hora e
Em determinada casa comercial, o número de traba- R ascunho lhadores do gênero masculino é 4 unidades menor que o número de trabalhadores do gênero feminino. Nessa casa comercial, cada trabalhador recebeu, no final do ano passado, como brinde, um vale-presente para ser utilizado na própria loja: para os homens, o vale-presente tinha valor unitário de R$ 120,00, e, para as mulheres, de R$ 150,00. Sabendo-se que ao todo foi distribuído um total de R$ 7.080,00 em vales-presentes, pode-se concluir corretamente que nessa casa comercial o valor total em vales-presentes distribuídos para os funcionários do gênero feminino foi de
Ney propôs a seus alunos um jogo. Cada um deveria pensar em um número inteiro e efetuar sucessivamente as seguintes operações: somar 5. multiplicar o resultado por 4. subtrair 8. dividir o valor obtido por 2. Depois, cada um diria o resultado em voz alta e ele adivinharia o número pensado. Para isso, em qualquer caso, é suficiente:
A fatoração tem, entre outras
características, a capacidade de simplificar
determinadas operações. Assim, o valor da
expressão
Navegando pelo Instagram encontra-se
essa “intervenção artística" feita em um piso
formado por lajotas na forma de hexágonos
regulares cujos lados medem 20 cm
A razão entre a área do triângulo em destaque e
área de um desses hexágonos e a razão entre os
perímetros dessas mesmas figuras são
respectivamente:
O número de divisores positivos do cubo da soma 111+222+333+444+555+666+777+888+999 é:
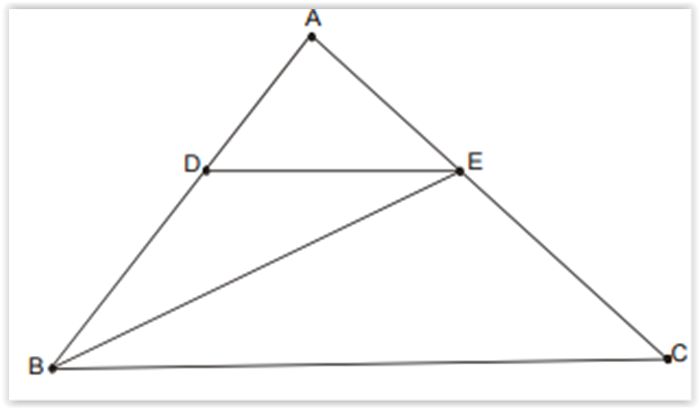
Na figura a seguir, o segmento DE é
paralelo ao lado BC. Sabendo-se que a razão entre
as áreas dos triângulos ADE e DBE vale 2/3, então
a razão entre as áreas dos triângulos ABC e EBC
vale:
Um grupo de pessoas apresenta as idades de 10, 13, 15 e 17 anos. Se uma pessoa de 12 anos se juntar ao grupo, o que acontecerá com a média de idade do grupo?