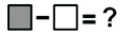Comprei uma mochila por R$ 40,00 na 25 de março em São Paulo e pretendo vendê-la por R$ 110,00. Qual a porcentagem de lucro colocada em cima desse produto?
Um engenheiro cria um gotejador para abastecer um bebedouro. Se, no primeiro segundo caem 3 gotas, no segundo 6 gotas, no terceiro 12 gotas, no quarto segundo 24 gotas e assim por diante, ao se passar um minuto e percebendo que o gotejador quebrou e parou o processo, neste caso, quantas gotas caíram no bebedouro até o processo parar?
Encontrando a relação entre p e n de modo que os coeficientes dos termos de ordem 5p e p + 4 da expressão (1 + x)2n sejam iguais, obtemos
Os critérios de avaliação na Matemática tem por objetivo apontar aspectos considerados essenciais em relação às competências que se espera que um aluno desenvolva até o final do primeiro ciclo. Como um desses critérios, podemos considerar:
O conjunto imagem da função quadrática f(x) = x² – 2x + 8 é expresso pelo intervalo:
O espaço compreendido por 1 terabyte (TB), unidade de medida para armazenamento digital, comporta cerca de 720 filmes, com 1h30min de duração cada. Quantos dias seriam necessários para projetar todos os filmes armazenados em 1 TB, sem intervalo entre um e outro?
O anfiteatro de certa faculdade possui 25 filas com 30 assentos cada. Sabendo que 1/3 dos lugares já está preenchido, e que 90 pessoas não irão comparecer ao evento, ainda restam chegar quantas pessoas?
Se x e y são dois números tais que x + y e x – y são dois números primos positivos distintos, então o número x² – y² é um número
O gráfico seguinte mostra parte do gráfico da função dada por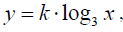 
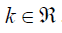
, em que 
. Sabendo que as abscissas de A e D são, respectivamente, 3 e 9, determine o perímetro do trapézio ABCD.
A função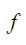 
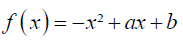
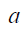
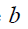
definida por 
tem valor máximo igual a 4 para x =1. Então, os valores dos parâmetros reais 
e 
são:
Ana, Bruno e Cássio são vizinhos há muito tempo e precisam entregar suas pesquisas estatísticas, juntamente com cópias de todas as pesquisas de campo realizadas. Ambos estavam com pressa, pois o prazo de entrega era curto e, portanto compraram o material necessário em uma mesma papelaria local.
Ana adquiriu 1 CD virgem e mais duas pastas, pagando pelo consumo R$ 5,50, enquanto Bruno precisou comprar 2 CDs e três pastas, pagando R$ 4,00 a mais que Ana.
Se Cássio comprar 1 CD e 5 pastas, pagando ao caixa, com uma nota de R$ 10,00, o troco que Cássio deverá receber é:
Um algoritmo precisa se completar, a fim de que uma programação seja finalizada com sucesso, e para tal, faz-se necessário calcular o somatório dos primeiros 30 números inteiros e consecutivos maiores que 50 e entrar com este valor na célula escura, em seguida deve-se entrar com o somatório dos 30 maiores números inteiros e consecutivos menores que 50, na célula branca.
da célula cinza pela célula branca, temos:
Carlos cadastrou uma senha de acesso à internet que equivale ao nono termo de uma P.G. (progressão geométrica) cujo primeiro termo é o número 3 e cuja razão é a mesma da P.A.(progressão aritmética): 12,14,....Nessas condições, a senha cadastrada por Carlos foi:
Para a resolução da questão a seguir, o candidato pode aproximar (1,03)3 por 1,1.
Um capital de R$ 1.200,00 foi aplicado em um sistema de juros compostos, cuja taxa de juros era de 3% ao mês, durante 6 meses. É correto afirmar que o montante obtido nesta aplicação é um valor compreendido entre:
