Em uma turma com 30 alunos, sendo 13 homens e 17 mulheres, deseja-se escolher, aleatoriamente, um representante, um vice-representante e um suplente, de modo que esse grupo não seja composto somente por homens e não seja composto somente por mulheres. O número total de possibilidades para fazer essa escolha é igual a
Em um papel em branco um aluno fez 15 pontos, entretanto, 6 pontos estão sobre uma mesma reta. Quantos triângulos distintos ele poderia fazer ligando quaisquer desses pontos?
Em um lote com 250 peças, foi constatado que existem exatamente seis defeituosas. Retirando-se, ao acaso, uma peça desse lote, a probabilidade de que ela seja perfeita é de _____%.
Dada a função f(x – 1) = x2 + 3x – 2, considerando os valores de f(1) e f(2), pode-se afirmar corretamente que
Seja a PG (a1, a2, a3, a4, ...) de razão q = 2. Se a1 + a5 = 272, o valor de a1 é
Considere a inequação x2 - 1 ≤ 3 . Está contido no conjunto solução dessa inequação o intervalo
Analise as quatro afirmações abaixo sobre uma matriz quadrada do tipo N x N:
I. O número de elementos fora da diagonal principal será N · (N -1).
II. Uma matriz N x N só pode ser multiplicada por uma outra matriz N x N.
III. O produto de uma matriz N x N por qualquer outra matriz sempre irá resultar em uma outra matriz quadrada.
IV. Toda matriz quadrada N x N é inversível.
Assinale a alternativa correta:
Um triângulo retângulo tem seus dois catetos com dimensões 12 cm e 20 cm. Sendo a o ângulo formado pelo cateto menor com a hipotenusa, assinale a alternativa correta acerca do valor do seno deste ângulo:
Cinco alunos serão divididos por sorteio em dois grupos da seguinte forma: o primeiro aluno sorteado será o líder do Grupo 1; o segundo aluno sorteado irá integrar o Grupo 1, junto com o primeiro aluno; o terceiro aluno sorteado será o líder do Grupo 2; os dois alunos restantes irão integrar o Grupo 2. Assinale a alternativa que indica de quantas formas esta divisão em grupos pode ocorrer.
Considere uma progressão geométrica com termo inicial igual a 1 e razão igual a 2, e uma progressão aritmética com termo inicial igual a 16 e razão igual a 8. Assinale a alternativa correta sobre os valores dos eventuais termos em comum destas progressões.
Considere uma sequência infinita de círculos: o primeiro tem raio R; o segundo, metade do raio do anterior (R/2); o terceiro, um quarto do raio do primeiro (R/4); e assim sucessivamente, cada círculo tendo metade do raio do círculo anterior. Assinale a alternativa que indica a soma das áreas de todos os círculos.
O consumo atual de água em uma cidade é 53.000.000 l/h. Suponha que este consumo cresça anualmente em 1,75 milhões l/h, e que este crescimento possa ser considerado como uma progressão aritmética. Se a capacidade de produção de água for de 78 mil m3/h, assinale a alternativa que apresenta em quantos anos, no máximo, será necessária a ampliação da capacidade de produção de água para que não ocorra falta de água.
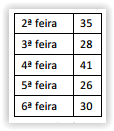
A tabela a seguir mostra o número de pessoas que visitaram certa empresa nos cinco dias da semana passada.
O número médio de visitas por dia é:
Moacir entrevistou os funcionários de uma empresa que foram admitidos nos últimos cinco anos e anotou o ano em que cada um ingressou na empresa.
O quadro abaixo mostra a marcação que Moacir fez para obter as quantidades de funcionários admitidos em cada ano a partir de 2012.
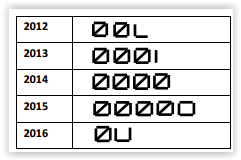
Desse grupo de funcionários, a porcentagem dos que foram admitidos depois de 2014 é:
Manoel cria coelhos e seus animais ou são brancos ou são marrons. Do total dos 120 coelhos que possui, 63 são fêmeas, 50 são marrons e, dos machos, 32 são brancos. O número de fêmeas marrons é: