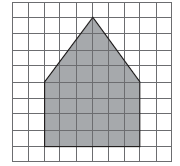
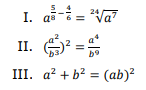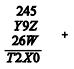Em uma malha quadriculada composta por 100 quadradinhos idênticos, foi desenhada e pintada uma figura de 5 lados, como se pode ver a seguir.
Assim, verifica-se que a região pintada corresponde a x% de toda a malha.
O valor de x é
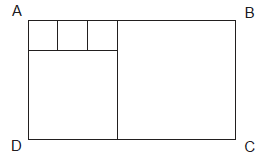
O retângulo ABCD é decomposto em cinco quadrados, como mostra a Figura.
Se o maior desses quadrados tem área igual a 100 cm2, então o perímetro do retângulo ABCD, em centímetros, é igual a
Marque a alternativa que apresenta o valor de k para que o vetor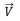 
seja uma combinação linear dos vetores 
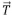e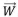 
.
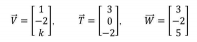
Considere 8 pontos distintos marcados na reta r e 5 pontos distintos marcados na retas. Sabendo-se que r e s são retas paralelas, qual o número total de triângulos que podem ser formados com vértices nesses pontos?
Observe a equação apresentada:
sen2(x) = 1
A solução da equação acima é:
Um tanque de água tem capacidade K. Após ficar completamente cheio, este tanque começou a escoar água perdendo 7% de seu volume a cada minuto. Qual será o volume de água no tanque daqui a t minutos?
Resolvendo-se a seguinte inequação do segundo grau:
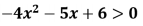
No conjunto dos números reais, obtém-se o conjunto solução
O resultado da divisão polinomial abaixo é indicado pela alternativa:
(3x8 -15x7 +x6 +20x5 -52x4 +8x3 +10x2 -2x)/(3x5 -2x3 +10x2 -2)
Dadas as sentenças abaixo:
Se
Dada a expressão 92x + 42x+1 + 53x e que x ∈ IN*, é correto afirmar que o resultado será:
Em se tratando de medidas de distância, 1 polegada equivale a:
As balanças a seguir estão em equilíbrio:
Nessas condições, o valor de x, em kg, que equilibra a terceira balança é:
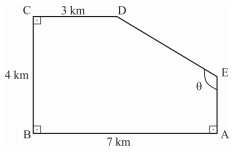
A figura seguinte ilustra um terreno pentagonal no qual será semeado um cultivar que, para desenvolver-se livre de parasitas, receberá a aplicação, para cada hectare, de 0,5 L de um herbicida especial cujo litro custa R$ 60.
Os cinco lados do terreno são retos e formam o pentágono ABCDE antecedente, em que os ângulos nos vértices A, B e C são retos, AB = 7 km, BC = 4 km e CD = 3 km. Sabe-se também que o ângulo no vértice E é θ, em que tg θ = –2 e tg (π – θ) = 2.
Na situação apresentada, o custo do herbicida a ser aplicado no terreno será de
Para a função ƒ(x) = αx2 + bx + c, em que α, b e c são constantes reais, tem-se que: ƒ(0) = 0, ƒ(10) = 3 e ƒ(30) = 15. Nesse caso, ƒ(60) é igual a
O professor de matemática de uma turma escreveu no quadro uma soma de três parcelas. Cada parcela era de três algarismos. Descuidadamente, um aluno apagou cinco algarismos. O professor, tentando recuperar a expressão original, escreveu, no lugar desses algarismos apagados, as letras T, W, X, Y e Z, como mostrado a seguir.
Considerando-se que o número XZ, em que Z é o algarismo da unidade e X é o algarismo da dezena, é maior que 9, então a soma T + W + X + Y + Z é igual a
