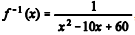Sendo X= 0,222 .. . e Y = 1,222 ... , o valor de 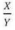
Considerando um período de 4 anos e uma taxa de juros simples de 1,2% ao mês, quanto deverá ser aplicado para, ao final deste período, gerar um rendimento de R$ 8.985,60?
Considere a seguinte situação hipotética: uma máquina é capaz de produzir 28 pratos descartáveis em 2 minutos. Considerando a mesma proporção, é correto afirmar que em 2 horas serão produzidos:
Qual o valor de k na equação de segundo grau: x2 + 6x + k + 2 = 0, de modo que as raízes reais sejam iguais.
Se x e y são números reais e soluções do sistema a seguir, então xy−1 é:
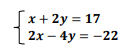
Qual a diferença entre o décimo segundo termo e o décimo quinto termo na sequência lógica a seguir: 10, 12, 13, 20, 22, 23, 30, 32, 33, 40, 42...
Qual o primeiro termo de uma progressão aritmética cuja a razão é −4 e o nono termo é −28.
Um número natural é expresso por 2+5x2-1. Qual o valor do antecessor desse número?
Ao passar com seu veículo por um radar eletrônico de medição de velocidade, o condutor percebeu que o velocímetro do seu carro indicava a velocidade de 99 km/h. Sabe-se que a velocidade mostrada no velocímetro do veículo é 10% maior que a velocidade real, que o radar mede a velocidade real do veículo, mas o órgão fiscalizador de trânsito considera, para efeito de infração, valores de velocidade 10% inferiores à velocidade real.
Nessa situação, considerando que a velocidade máxima permitida para a via onde se localiza o referido radar é de 80 km/h,
o condutor não cometeu infração, pois, descontando-se 20% da velocidade mostrada no velocímetro de seu veículo, o valor de velocidade considerada pelo órgão fiscalizador será de 79 km/h.
A probabilidade de sair soma 7 no lançamento de dois dados é:
Foi distribuído um bônus de R$ 15 000,00 entre os três melhores funcionários de uma empresa. Se um deles recebeu 20% desse valor, o outro recebeu 45%, o terceiro recebeu, em reais:
A metade de 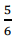 é:
é:
Quantos são os gabaritos possíveis de um concurso com 20 questões de múltipla-escolha, com 4 alternativas por questão?
O número de Euler, nome dado em homenagem ao matemático suíço Leonhard Euler, é um número irracional denotado por e, cuja representação decimal tem seus 4 primeiros algarismos dados por 2,718. Esse número é a base dos logaritmos naturais, cuja função f(x) = lnx = logex tem inúmeras aplicações científicas.
A respeito desse assunto, julgue o item a seguir.
A função exponencial g(x) = ex , função inversa de ln x, é uma função crescente.
Cada j = 0, 1, …, 11 representa um mês do ano de 2017, isto é, j = 0 = janeiro, j = 1 = fevereiro, e assim sucessivamente. Se o mês j tem d dias, então j + 1/d representa o dia 1.º do mês j; j + 2/d representa o dia 2 do mês j, e assim sucessivamente, j + d/d = j + 1 representa o dia d do mês j. Dessa forma, cada dia do ano de 2017 pode ser representado por um número x do intervalo [0, 12]. Considere que, nessa representação, em cada dia x do ano de 2017, a porcentagem de água acumulada em relação à capacidade máxima do reservatório de determinada represa seja expressa pelo valor da função f(x) = x2 - 10x + 60.
A partir dessas informações, julgue o item que se segue.
A inversa de
f(x) é expressa por