Pedro tinha uma quantia no banco. Na segunda-feira ele retirou R$ 150,00 e na terça-feira fez um depósito de R$ 90,00. Com isso, seu saldo ficou de R$450,00. Qual é a quantia que ele tinha inicialmente no banco?
Para fazer um doce de banana, deve-se usar 0,625 kg de açúcar para cada quilo de bananas. A quantidade aproximada (com erro de, no máximo, 3 g da quantidade exata) de açúcar, em kg, que se deve usar para fazer um doce com 3,5 kg de bananas é
Um hospital realizou um concurso oferecendo vagas para os cargos de técnico em enfermagem e de administração hospitalar. Inscreveram-se 120 candidatos, sendo que o número de mulheres foi o dobro do número de homens.
O quadro incompleto a seguir mostra os números de candidatos aos dois cargos:
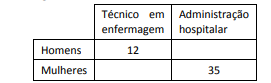
O número total de candidatos para técnico em enfermagem era de
50 atletas estão treinando e todos usam bermuda e camiseta do mesmo modelo, mas com cores diversas. Entre esses atletas há 20 com bermudas brancas, 25 com camisetas brancas e 12 com bermudas e camisetas brancas.
Assinale a opção que indica o número de atletas que não estão vestindo nenhuma peça branca.
Certo arquiteto planejou colocar no aeroporto da cidade uma faixa muito comprida com as seguintes letras em sequência, mantendo sempre o mesmo padrão:
SALVADORBAHIASALVADORBAHIASALVADORBA...
A 500ª letra dessa sequência é
Em uma padaria são produzidos 100 pães de 32 gramas cada um. Caso queira produzir pães de 20 gramas cada um, quantos iremos obter?
O sistema linear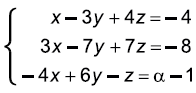
terá solução somente quando o valor de α for igual a
Os gráficos a seguir apresentam a safra de grãos e a área plantada no Brasil, no período de 2010 a 2018.
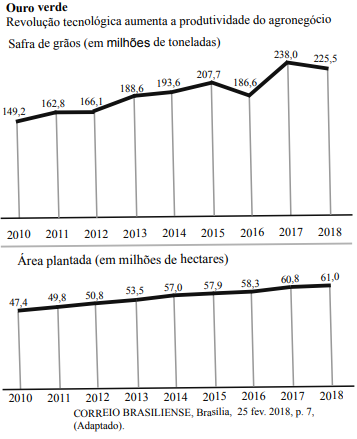
De acordo com as informações apresentadas nos gráficos, a produtividade média por hectare
Os números inteiros x, y e z são tais que
x – 2y = 2z – 1; z + x = y - 2 e 2x + y + 3z = 1.
Nessas condições. é CORRETO afirmar que:
Dado dois conjuntos, A e B, assinale a alternativa INCORRETA em relação as operações entre conjuntos:
Dados os conjuntos A { 2,3,4,5,6} e B { -1,0,2,3} assinale a alternativa INCORRETA :
Pamela tem uma filha de 15 anos e sua idade é triplo de sua filha, quantos anos tem Pamela?
Assinale a alternativa que corresponde ao máximo divisor como entre 2, 6.
Vilma tem 70 anos e Gisele tem 20% da idade de Vilma, qual a idade de Gisele?
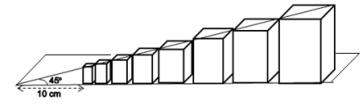
Um professor de matemática tirou o final de semana para organizar sua estante de livros e em uma das prateleiras ele usou a seguinte formação: foram dispostos oito livros, um ao lado do outro, de acordo com suas respectivas espessuras e alturas, de modo que um sempre tivesse o dobro da espessura do outro e o da frente seja sempre maior que o de trás, formando com a base da prateleira onde estavam, um triangulo retângulo com um ângulo de 45º, como expresso na figura abaixo. Qual a altura, em metros, do maior livro, sabendo que o menor livro mede 0,2cm de espessura?
Dados: use √3 = 1,7.
