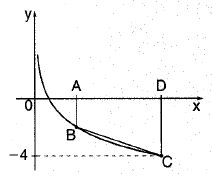
O gráfico seguinte mostra parte do gráfico da função dada por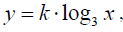 
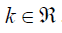
, em que 
. Sabendo que as abscissas de A e D são, respectivamente, 3 e 9, determine o perímetro do trapézio ABCD.
A função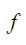 
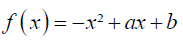
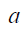
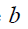
definida por 
tem valor máximo igual a 4 para x =1. Então, os valores dos parâmetros reais 
e 
são:
Ana, Bruno e Cássio são vizinhos há muito tempo e precisam entregar suas pesquisas estatísticas, juntamente com cópias de todas as pesquisas de campo realizadas. Ambos estavam com pressa, pois o prazo de entrega era curto e, portanto compraram o material necessário em uma mesma papelaria local.
Ana adquiriu 1 CD virgem e mais duas pastas, pagando pelo consumo R$ 5,50, enquanto Bruno precisou comprar 2 CDs e três pastas, pagando R$ 4,00 a mais que Ana.
Se Cássio comprar 1 CD e 5 pastas, pagando ao caixa, com uma nota de R$ 10,00, o troco que Cássio deverá receber é:
Um algoritmo precisa se completar, a fim de que uma programação seja finalizada com sucesso, e para tal, faz-se necessário calcular o somatório dos primeiros 30 números inteiros e consecutivos maiores que 50 e entrar com este valor na célula escura, em seguida deve-se entrar com o somatório dos 30 maiores números inteiros e consecutivos menores que 50, na célula branca.
da célula cinza pela célula branca, temos:
Carlos cadastrou uma senha de acesso à internet que equivale ao nono termo de uma P.G. (progressão geométrica) cujo primeiro termo é o número 3 e cuja razão é a mesma da P.A.(progressão aritmética): 12,14,....Nessas condições, a senha cadastrada por Carlos foi:
Em cada item a seguir é apresentada uma situação hipotética, seguida de uma assertiva a ser julgada, a respeito de modelos lineares, modelos periódicos e geometria dos sólidos.
O tanque para água de um veículo de combate a incêndio tem a forma de um paralelepípedo retângulo e está completamente cheio. No combate a um incêndio, gastou-se 1/3 de sua capacidade. No combate a um segundo incêndio, gastou-se 3/7 do que sobrou. Nesse caso, depois de extintos os dois incêndios, restou, no tanque, água até uma altura superior a 1/3 da altura original.
Em um tanque A, há uma mistura homogênea de 240 L de gasolina e 60 L de álcool; em outro tanque B, 150 L de gasolina estão misturados homogeneamente com 50 L de álcool.
A respeito dessas misturas, julgue o item subsequente.
Considere que em um tanque C, inicialmente vazio, tenham sido despejadas certas quantidades das misturas dos tanques A e B totalizando 100 L. Considere também que, depois de homogeneizada essa mistura no tanque C, a separação de álcool e gasolina por um processo químico tenha mostrado que nesses 100 L, 22 L eram de álcool. Nessa situação, para formar essa mistura no tanque C foram usados mais de 55 L da mistura do tanque A.
A metade da medida do ângulo interno de um octógonoregular, em graus, é
Sejam os números complexos z1 = 1 – i, z2 = 3 + 5i e z3 = z1 + z2. O módulo de z3 é igual a
As funções f(x) = sen x e g(x) = cos x, no segundo quadrante, são, respectivamente,
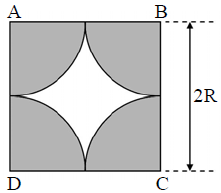
Na figura, os arcos que limitam a região sombreada são arcos de circunferências de raio R e centrados nos vértices do quadrado ABCD. Se o lado do quadrado mede 2R e considerando π = 3, então a razão entre a área sombreada e a área branca é
Josué fez uma viagem em 3 horas e 20 minutos, e a cada hora percorria 45 km. Voltou, pelo mesmo percurso, com velocidade constante e gastando 20% a menos do tempo da viagem de ida. Na volta, a cada hora, Josué percorria
Para ir ao trabalho caminhando, Rodrigo percorreu a terça parte do percurso sem qualquer parada. Descansou um pouco e, em seguida, percorreu a quinta parte do que
restava do percurso e, novamente, parou para descansar. Após essas duas etapas, ainda faltavam 1 080 metros para Rodrigo chegar ao destino. A diferença entre o número de metros que Rodrigo caminhou na primeira etapa em relação à segunda etapa é igual a
Em determinado concurso público para o cargo de professor,
1.200 candidatos inscreveram-se para as áreas de física,
matemática e química. Sabe-se que, dos inscritos, 230 podem
lecionar matemática e física; 380 podem lecionar física e
química; 220 podem lecionar matemática e química; 560
podem lecionar matemática; e 120 podem lecionar as três
disciplinas. A partir dessas informações, é possível construir o
denominado diagrama de Euler-Venn, como mostra a figura
a seguir.
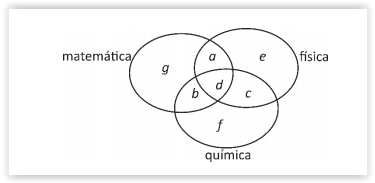
O diagrama mostra subconjuntos disjuntos e cada uma das
letras de a a g indica a quantidade de elementos do
respectivo subconjunto. Por exemplo, g é a quantidade de
inscritos que só lecionam matemática. Com base nessas
informações e no diagrama, julgue os itens seguintes.
Mais de 200 inscritos podem lecionar apenas matemática.
Na figura a seguir, as retas r1, r2, r3, r4 e r5 são paralelas; as
retas s1 e s2 são transversais; X, Y e Z e os números ao lado
dos segmentos das retas transversais indicam seus
respectivos comprimentos.
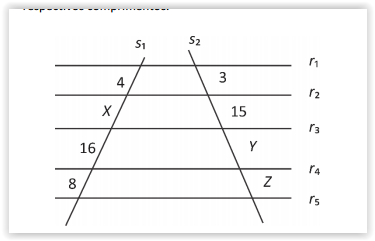
Com relação à figura, julgue os itens seguintes.
X + Z = 23.
