Analisar os itens abaixo:
I - Para os conjuntos A = {1, 2, 3, 4} e B = {3, 4, 5, 6}, a intersecção dos conjuntos pode ser representada por A ∩ B = {3, 4}.
II - Para os conjuntos A = {j, k, l, m} e B = {m, o, p, q}, a união dos conjuntos pode ser representada por A ∪ B = {j, k, l, m, o, p, q}.
III - Para os conjuntos A = {20, 40, 60, 80} e B = {40, 60, 80, 100, 120}, a união dos conjuntos pode ser representada por A ∩ B = {40, 60, 80}, e a intersecção dos conjuntos pode ser representada por A ∪ B = {20, 40, 60, 80, 100, 120}.
IV - Para os conjuntos A = {f, g, h} e B = {v, x, w}, a intersecção pode ser representada por A ∩ B = {f, g, h, v, x, w}.
Está(ão) CORRETO(S):
Considerando-se as unidades de medida de capacidade, área e volume, marcar C para as afirmativas Certas, E para as Erradas e, após, assinalar a alternativa que apresenta a sequência CORRETA: (---) Para determinada dose de certa vacina, é necessário tomar 15mL de medicação, que deverá ocupar um volume equivalente a 15cm³. (---) Fernando tem dois terrenos, sendo um deles de área de 1.800.000cm² e o outro de 0,00023km². Ao se somar as áreas dos dois terrenos, a área total será igual a 410m². (---) Em certa solução, para cada litro de água, é necessário colocar 50mL de água sanitária. Se for utilizado um litro de água sanitária, serão necessários 200L de água.
Considerando-se que A = 68, B = 75, C = 80 e D = 82, analisar os itens abaixo: I - A razão entre A e D é igual a 34/41. II - A razão entre B e A é igual a 15/17. III - A razão entre C e D é igual a 40/41. IV - A razão entre B e C é igual a 15/16. Estão CORRETOS:
A soma dos primeiros 38 termos da sequencia 5, 12, 19, 26, ..., é:
Com relação a proporcionalidade, regras de três e divisão de grandezas, julgue os itens que se seguem.
Supondo-se que x = 30, y = 15 e x = cy, a constante de
proporcionalidade c será igual a 2.
Qual é a soma dos 17 primeiros termos em
uma progressão Aritmética, sendo o primeiro
termo a1 = 13 e o décimo a17 = 45
Em determinado concurso público para o cargo de professor,
1.200 candidatos inscreveram-se para as áreas de física,
matemática e química. Sabe-se que, dos inscritos, 230 podem
lecionar matemática e física; 380 podem lecionar física e
química; 220 podem lecionar matemática e química; 560
podem lecionar matemática; e 120 podem lecionar as três
disciplinas. A partir dessas informações, é possível construir o
denominado diagrama de Euler-Venn, como mostra a figura
a seguir.
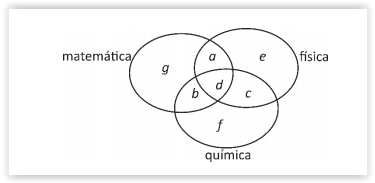
O diagrama mostra subconjuntos disjuntos e cada uma das
letras de a a g indica a quantidade de elementos do
respectivo subconjunto. Por exemplo, g é a quantidade de
inscritos que só lecionam matemática. Com base nessas
informações e no diagrama, julgue os itens seguintes.
A partir do diagrama, é possível construir um sistema de equações lineares nas variáveis de a a g, sendo que, nesse caso, a solução desse sistema é única.
Uma sala retangular medindo 18 m × 30 m deverá servir para
pequenos eventos. O projeto dessa sala inicialmente previa a
sua divisão em quadrados de mesmo tamanho e de área
máxima, de modo que, em cada um desses quadrados, fosse
colocada uma mesa redonda com cadeiras à sua volta. A
respeito desse projeto, julgue os itens que se seguem.
Considerando-se que o projeto preveja um corredor lateral de 1 m de largura que acompanhe as quatro paredes da sala, ficando o espaço interno restante para a desejada divisão em quadrados iguais e de área máxima, a divisão será feita em mais de 25 quadrados e cada um deles terá área superior a 17 m2.
Na figura a seguir, as retas r1, r2, r3, r4 e r5 são paralelas; as
retas s1 e s2 são transversais; X, Y e Z e os números ao lado
dos segmentos das retas transversais indicam seus
respectivos comprimentos.
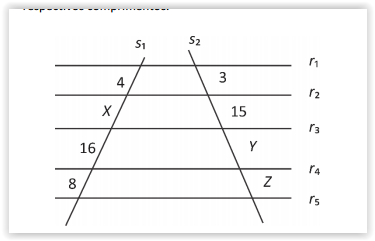
Com relação à figura, julgue os itens seguintes.
X + Y = 31.
Os professores João, Paulo e Pedro participaram de uma
maratona que consistia em correr ao redor de uma pista
circular em um parque da cidade. Partindo do ponto inicial,
João deu uma volta no parque em 8 minutos; Paulo fez o
mesmo em 12 minutos e Pedro, em 15 minutos.
Considerando que eles partiram do ponto inicial juntos e no
mesmo instante, julgue os itens a seguir.
Paulo e Pedro passaram juntos pelo ponto inicial antes de 60 minutos de iniciada a corrida.
Em uma sala de aula, entre alunos e alunas, há 36 pessoas.
Se, em determinado dia, seis das alunas faltarem às aulas e
todos os alunos se fizerem presentes, então, nesse dia, a
quantidade de alunos será o dobro da de alunas. Um
problema que se coloca é determinar quantos alunos e
quantas alunas pertencem a essa sala.
A respeito dessa situação hipotética, julgue os itens
subsecutivos.
Nessa sala, a diferença entre as quantidades de alunos e de alunas é superior a cinco.
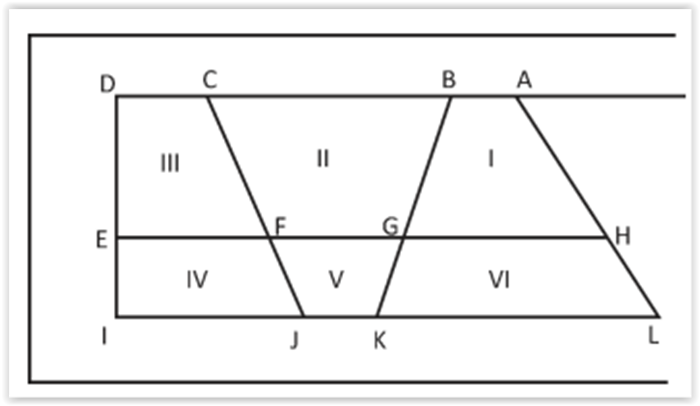
A figura a seguir mostra um projeto para um pavilhão de salas de aula de uma escola. Com a previsão de construção de uma sala para vídeos, como a sala indicada por II, e outra para depósito, como a indicada por V, algumas salas perderam a forma normal retangular. A figura a seguir mostra a disposição das salas de I a VI, que serão acessadas por corredores.
Os segmentos AD, EH e IL são paralelos entre si; o lado DI é perpendicular a AD, a EH e a IL. Algumas medidas são: AD = 20 m; DE = 8 m; e EI = 4 m.
Os ângulos BCJ e CBK são iguais a 60°.
Tendo como referência a figura apresentada e as medidas fornecidas, julgue os itens que se seguem.
O projeto poderá ser executado de acordo com a figura se prever que a medida de BC seja igual a 10 m.
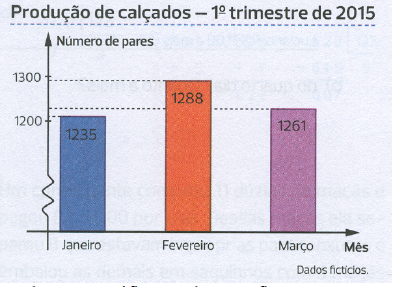
O gráfico abaixo mostra a produção de uma fábrica de calçado no 1º trimestre de 2015.
Com base no gráfico, podemos afirmar que para que a produção do trimestre chegue a 4000 pares faltam quantos pares?
Imagine uma figura onde está representado um círculo com um quadrado inscrito. Escolhendo, ao acaso, um ponto do círculo a probabilidade desse ponto pertencer ao quadrado é?
Uma caixa de luvas contém 24 pares. Qual das alternativas abaixo representa uma quantidade que pode ser obtida comprando-se uma certa quantidade de caixas?