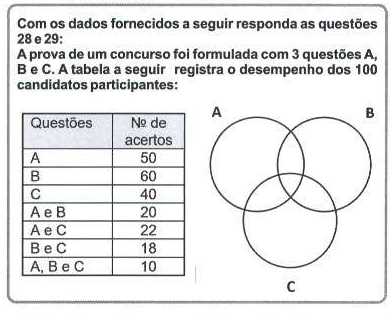
Em uma escola com 630 alunos, 435 deles estudam Matemática, 319 deles estudam Física e 187 deles estudam as duas matérias (Matemática e Física). Com base no exposto a probabilidade de um aluno escolhido ao acaso não estudar nenhuma das matérias (Matemática e Física) é igual à:

Um administrador calcula a probabilidade de sua empresa ganhar, ao menos, uma das três licitações em que está concorrendo. Sabe-se que as licitações são independentes e que a probabilidade de ganhar as licitações A, B e C são, respectivamente, 20%, 35% e 10%.
Qual a probabilidade de a empresa vencer pelo menos uma licitação?
Em uma cidade, 80% das famílias têm televisão e 35% têm microcomputador. Sabe-se que 90% das famílias têm pelo menos um desses aparelhos. Se uma família for escolhida aleatoriamente, a probabilidade de ela ter ambos os aparelhos é igual a
Treze carros de mesmo modelo serão aleatoriamente enfileirados, lado a lado. Quatro deles são azuis, três são pretos, cinco brancos e um vermelho. Cada carro tem uma numeração que também será registrada em um cartão, e estes, colocados em uma mesma urna. Ao se retirar aleatoriamente os cartões, um a um, identifica-se o carro e o estaciona. Qual a probabilidade de que todos os carros de mesma cor fiquem juntos?
João e Adilson estão em uma reunião com todos os outros supervisores da empresa em que trabalham. Eles estão sentados juntos a uma mesa retangular, cada um (João e Adilson) em uma ponta. Entre eles, de um lado, há três pessoas e, do outro, duas pessoas. Um garçom coloca, aleatoriamente, 7 pratos na mesa, um na frente de cada lugar. Em um desses pratos, está colado um envelope com a quantia de R$ 1.000,00. Qual é a probabilidade de João ou Adilson receberem o prato com o envelope?
A respeito do princípio da contagem, de permutações e de probabilidade, julgue o item. Escrevendo‐se cada letra da palavra AUXILIAR em uma bola e colocando as oito bolas em uma urna, a probabilidade de se retirar duas bolas e ambas serem consoantes é superior a 12%.
João vai viajar e precisa escolher 3 camisas para levar. Sabendo-se que ele dispõe de 5 camisas distintas para escolher, ao todo, de quantas formas distintas ele pode fazer essa escolha?
Em uma mostra de cinema, há 6 filmes para serem exibidos em 6 dias, cada filme em um dia diferente. Há 3 filmes de comédia e 3 de terror. Com base nessa situação hipotética, julgue o item.
Se um crítico escreveu resenhas para 3 filmes da mostra de cinema, então a probabilidade de ele ter escrito resenhas exatamente para os 3 filmes de comédia é menor que 4%.
Uma construtora comprou um grande lote de peças de mármore diretamente de uma grande marmoraria para a construção de casas populares. As peças vêm embaladas de forma individual. Um funcionário da construtora inspeciona cinco peças para verificar o número de peças quebradas ou danificadas. A perda de materiais na construção civil é bastante elevada. Os percentuais de perdas de alguns materiais preocupam as empresas. Sabendo-se que um grande lote contém 1% de peças quebradas ou danificadas, analise as seguintes afirmativas:
- A probabilidade de o funcionário encontrar no máximo uma peça quebrada ou danificada é 1,04x(0,99)4 .
- A probabilidade de o inspetor encontrar pelo menos uma peça quebrada ou danificada é 1 − 0,995 .
- A probabilidade de o inspetor encontrar todas as peças defeituosas é (0,01)2
Seja P( X ) a probabilidade de ocorrência de um evento X. Dados 2 eventos A e B, a probabilidade de ocorrer pelo menos um dos dois eventos é igual a 4/5 e a probabilidade de ocorrer o evento A e o evento B é igual a 1/10. Se P( A ) é igual a 1/2, então P( B ) é igual a
Pesquisa realizada com um grupo de 100 pessoas jovens de uma cidade do interior do Estado de São Paulo mostrou que:

Com base nessa pesquisa, qual é a probabilidade de que ao se escolher, aleatoriamente, uma dessas pessoas, de que a pessoa escolhida seja um jovem graduado fumante ou um jovem não fumante?
No Pisa, avaliação internacional da OCDE, o cenário é difícil para jovens de 15 a 16 anos. Desde 2009, o Brasil não apresenta avanços nesta avaliação. Com o gráfico abaixo vemos a evolução da média do Brasil em Matemática no Pisa. Temos um grande desafio - 46,5% de nossos alunos na rede pública estão abaixo do nível 1 em Matemática.
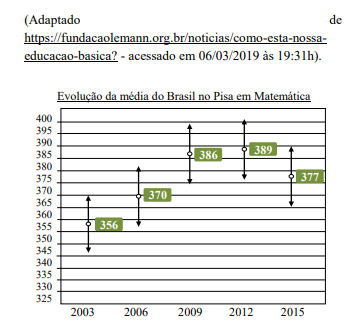
Seja xi a média em Matemática obtida pelo Brasil no Pisa e
Num programa de TV tem um quadro que premia participantes previamente selecionados. O melhor dos prêmios é um carro zero quilômetro. Para ganhar esse prêmio o participante tem que girar três vezes uma roleta com numeração de 1 a 10. Se a soma dos números obtidos nos três giros for menor que 10, o participante leva o prêmio. Ao girar a roleta três vezes, qual a probabilidade de um participante ganhar o carro?