Na figura a seguir, o quadrado PMNQ está inscrito em outro
quadrado ABCD, cujos lados medem 16 cm.
De acordo com essas informações, o menor valor, em cm,
que o segmento MB pode assumir para que a área do
quadrado PMNQ seja 136 cm2 deve ser igual a:
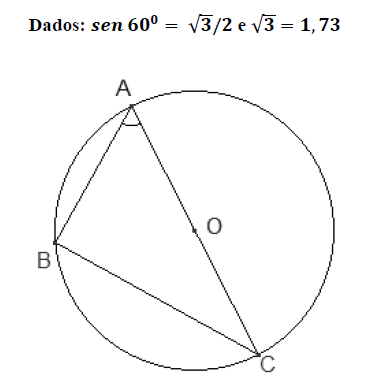
A figura a seguir representa um triângulo ABC, inscrito numa circunferência de centro O, raio igual a 4 cm e ângulo  medindo 60o. Se um dos lados do triângulo é um diâmetro da circunferência, qual é a medida aproximada de sua área?
Considere o seguinte polígono em que todas as medidas são dadas em metro.
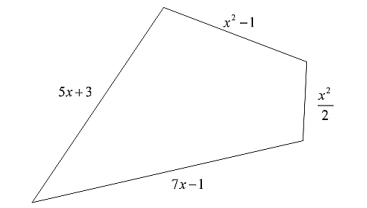
Sabendo que o perímetro deste polígono é 73 m, conclui-se que o valor de x é
A quantidade de retângulos com lados de comprimento inteiro
que é possível formar, tendo sempre um perímetro de 24 cm, é
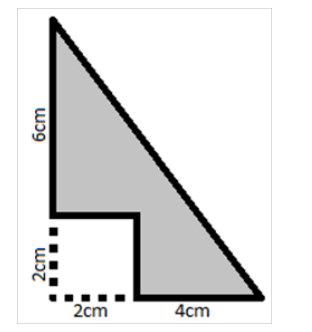
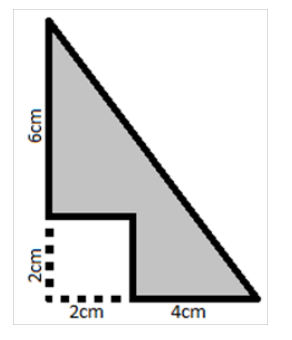
Qual a área sombreada da figura a seguir?
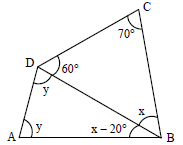
No quadrilátero ABCD, o valor de y – x é igual a
Ao somar o número de diagonais e o número de lados de um dodecágono obtém-se
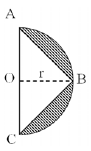
Na figura, O é o centro do semicírculo de raio r = 2cm. Se A, B e C são pontos do semicírculo e vértices do triângulo isósceles, a área hachurada é _______ cm². (Use π = 3,14 )
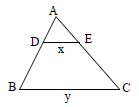
Seja um triângulo ABC, conforme a figura. Se D e E são pontos, respectivamente, de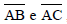 
de forma que AD = 4, DB = 8, DE = x, BC = y, e se 
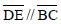, então
Seja um triângulo inscrito em uma circunferência de raio R. Se esse triângulo tem um ângulo medindo 30°, seu lado oposto a
esse ângulo mede
Seja ABCD um paralelogramo cujos lados são AB , BC , CD e DA . Prolongando-se o lado CD
até o ponto P obtém-se o triângulo Δ APD e traçando a diagonal BD obtém-se o triângulo Δ CD,
cujo ângulo ˆCBD é congruente ao ângulo APˆD , conforme a figura mostra.
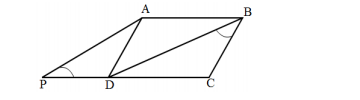
Sabendo que a medida de AB = 9 cm e que a medida de DP = 4 cm. Pode-se dizer que a medida
do perímetro do paralelogramo é igual a
As figuras a seguir foram construídas sobre papel quadriculado.
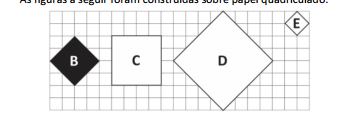
Sobre as figuras B, C, D e E, assinale a afirmativa correta.
Para trabalhar um conceito ainda pouco conhecido por seus
alunos, o professor exibiu contraexemplos relacionando
características de alguns polígonos. Para isso, preparou o
seguinte exercício para seus alunos:
Observe as figuras a seguir.
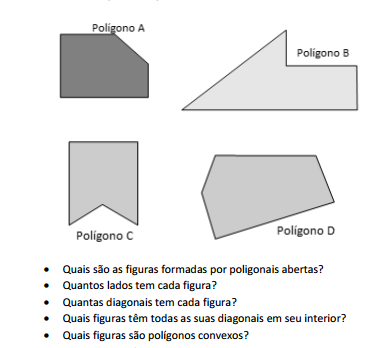
Essa questão envolveu os seguintes conceitos:
Qual a área sombreada da figura a seguir?
Na figura abaixo, ABCDEF é um hexágono regular de lado a inscrito numa circunferência. Sabendo
que, AB ≅ BC ≅ CD ≅ DE ≅ EF ≅ FA são arcos da circunferência cujo raio mede r
A
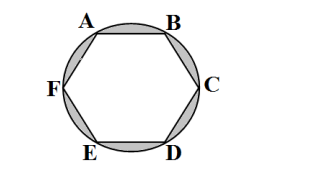
A razão entre a área hachurada nessa figura e a área da circunferência em que o hexágono está
inscrito é igual a: (Use √3 = 1,7 e π = 3)
