A figura seguinte mostra, em um sistema de coordenadas cartesianas ortogonais xOy, em que a unidade de medida é o metro, uma região retangular OABC. O lado OA mede 600 m e o lado OC mede 800 m.
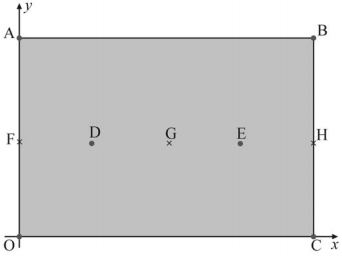
A figura mostra também os pontos F = ponto médio de OA, H = ponto médio de CB, G = centro do retângulo OABC, D = ponto médio de FG, e E = ponto médio de GH. Nos pontos O, A, B, C, D e E foram instalados pontos de acesso à Internet — wi-fi. Nessa configuração, o usuário consegue se conectar à Internet desde que o seu smartphone esteja a 200 m ou menos de qualquer desses pontos de acesso.
Com base nessas informações e na figura apresentada, julgue o próximo item.
A reta que contém os pontos B e E intercepta o eixo Ox no ponto de abscissa x = 300.
A Torre do Big Ben, em Londres, construída em 1858, é um edifício de 106 metros de altura no estilo gótico, com quatro relógios, cada um com sete metros de diâmetro. Trata-se de um dos relógios mais confiáveis que existem e símbolo da pontualidade britânica. Representando por (x(t), y(t)) a extremidade móvel do ponteiro que marca as horas num dos relógios da Torre do Big Ben, sabendo-se que o comprimento do ponteiro é 2,7 metros, o tempo é medido em segundos a partir de 15:00 e a origem do sistema de coordenadas é no centro do relógio, temos que as equações paramétricas de x(t) e y (t) são
Sobre um mapa de uma região, foi aplicado um sistema de coordenadas cartesianas, em que cada segmento de medida unitária, nesse sistema, correspondia a 1,5 quilômetros reais e, nesse sistema, duas praças foram identificadas com as coordenadas (1, –3) e (4, 1).
A distância real, em linha reta, em quilômetros, entre essas praças é de
Considere as seguintes relações em IR 2:
I)
Sendo A(2,4) e B(-1,3) pontos no plano cartesiano. Qual a distancia entre A e B?
Um triângulo retângulo tem sus vértices nos pontos de coordenadas cartesianas (0 , 0), ( 3 , 0 ) e ( 0 , 4 ). O perímetro deste triângulo mede:
João desejava fazer o desenho de uma circunferência, cujo centro
C é ponto do 2° quadrante do Plano Cartesiano. Esta circunferência também deverá ser tangente ao eixo das ordenadas e possuir obrigatoriamente 2 pontos de intersecção (A e B) com o eixo das abscissas, sendo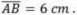 
Ao iniciar o seu esboço percebeu que o centro C desta circunferência poderia estar em inúmeros lugares distintos deste Plano.
Desta forma, pode-se afirmar que o lugar geométrico de todos os pontos, onde C poderia estar localizado é uma:
O resultado da soma de todas as coordenadas dos pontos de interseção de L1 com os eixos coordenados é
Considere a circunferência dada por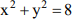 
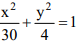
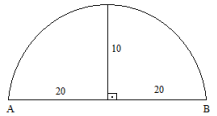
e a elipse dada por 
. A circunferência e a elipse se interceptam em quantos pontos?
Considere o arco de circunferência entre os pontos A e B de acordo com a figura a seguir. O raio da circunferência que tem este arco mede
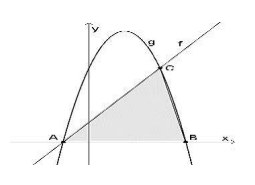
A figura a seguir apresenta os gráficos de duas funções f e g, afim e quadrática, respectivamente. Os vértices do triângulo ABC pertencem ao gráfico da função g(x) = -2x2 + 4x + 4. Sabendo que a área desse triângulo é 4√3 unidades quadráticas, o coeficiente angular da função f é:
Considere o triângulo ABC com vértices A = (- 6, - 2), B = ( 6, 1) e C = ( 2, 4). Prolonga-se os segmento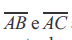 
a partir dos pontos B e C, respectivamente. Em seguida trace uma bissetriz exterior a partir do ponto C até interceptar o prolongamento do segmento 
no ponto Q.Determine a área do triângulo ACQ, a qual vamos denotar por S, sabendo que as medidas são dadas em metros e indique o resultado
CORRETO:
Considere a parábola definida por y = x2 – 4x +7 e a circunferência definida por (x -2)2 + (y -3)2 = 4. Assinale a alternativa que indica em quantos pontos estas duas curvas se interceptam.
Se r: 4x - 3y + 15 = O é uma reta contida no plano R² calcule a distância entre r e o ponto P (1 , -2).
