O próximo item apresenta uma situação hipotética seguida de uma assertiva, a ser julgada com base na matemática e em suas aplicações na atividade policial.
Em uma cidade, existem três antenas de celular — A, B e C —, representadas em um plano cartesiano de tal forma que A(0, 0), B(2, 0) e C (1/2 , √3/2 ), em que as unidades estão em quilômetros. As antenas A e B captam um telefone celular que está em um ponto P(x0, y0) localizado a 2 km de distância de cada uma delas, e a antena C também recebe sinal desse aparelho. Nesse caso, sabendo-se que y0 > 0, conclui-se que a distância entre P e C é igual a 1 km.
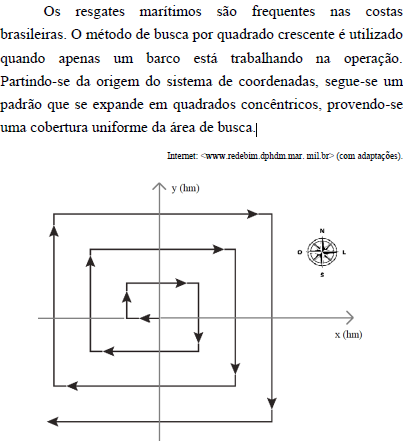
O gráfico anterior ilustra, em um sistema de coordenadas cartesianas ortogonais xOy, parte da trajetória percorrida por determinado barco que realizou o método de busca por quadrado crescente descrito no texto precedente. Os dois primeiros movimentos desse barco — primeiro para o oeste e depois para o norte — têm comprimentos iguais a 1 hectômetro (hm); os dois próximos movimentos têm comprimentos iguais a 2 hm; os dois movimentos seguintes a estes têm comprimentos iguais a 3 hm; e assim sucessivamente.
Considerando as informações apresentadas, julgue o item subsequentes, a partir dessa situação hipotética
A curva de equação
A circunferência que tem seu centro no ponto (1 ,−1) e é tangente à reta de equação tem equação dada por
Leia o texto a seguir para julgar o item 27:
Numa ampliação ou redução de figuras geométricas planas, os lados conservam a mesma forma, mas não o mesmo comprimento. Para que duas figuras geométricas planas sejam semelhantes, elas precisam ter ângulos congruentes, isto é, de mesma medida e lados proporcionais.
(Fonte: adaptado de http://clubes.obmep.org.br/blog/sala-para-leitura_032-ampliar-ou-reduzir-eis-a-questao/. Acesso em agosto de 2021)
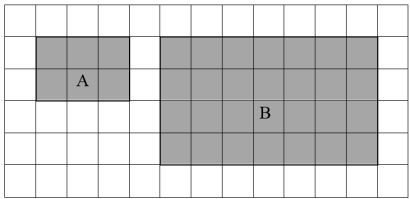
As imagens a seguir mostram dois retângulos construídos em malha quadriculada. Podemos dizer que o retângulo B representa uma ampliação do retângulo A, pois atende ao conceito de semelhança.

O gráfico anterior ilustra, em um sistema de coordenadas cartesianas ortogonais xOy, parte da trajetória percorrida por determinado barco que realizou o método de busca por quadrado crescente descrito no texto precedente. Os dois primeiros movimentos desse barco — primeiro para o oeste e depois para o norte — têm comprimentos iguais a 1 hectômetro (hm); os dois próximos movimentos têm comprimentos iguais a 2 hm; os dois movimentos seguintes a estes têm comprimentos iguais a 3 hm; e assim sucessivamente.
Considerando as informações apresentadas, julgue o item subsequentes, a partir dessa situação hipotética
Os vértices da trajetória do barco que estão localizados nos dois primeiros quadrantes pertencem à reta
Dadas as retas r: 2x − 3y + 9 = 0, s: 8x − 12y + 7 = 0 e t: 3x + 2y − 1 = 0, pode-se afirmar, corretamente, que
Uma circunferência tem centro na origem do sistema cartesiano e passa pelo ponto (0,3). Nessas condições, a equação e o comprimento dessa circunferência são, RESPECTIVAMENTE:
Se um ponto móvel se deslocar, em linha reta, do ponto A(0, 0) para o ponto B(4, 3) e, em seguida, para o ponto C(7, 7), então ele percorre uma distância de ___________ unidades de comprimento.
Em uma das aulas de Geometria Analítica, o professor solicitou que cada estudante fizesse apontamentos a partir da reta que passa pelo ponto P (3; 6) e forma, com o eixo das abscissas, 135°. Eis as informações que recebeu.
- Amanda: O coeficiente angular da reta é -1.
- Beatriz: A reta passa pelo ponto F(-3; -6).
- Cecília: A reta é concorrente ao eixo x.
- Daiana: Todo ponto de ordenada igual a 6 pertence a reta.
Nessas condições, pode-se afirmar que:
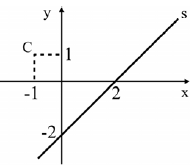
Sejam o ponto C e a reta s de equação(s) x − y − 2 = 0, representados na figura. O quadrado do raio da circunferência de centro C e tangente à reta s é
Em uma brincadeira de acertar alvos existem, pintadas no chão, duas circunferências distintas, uma com 20 cm e outra com 40 cm de diâmetro. O jogo consiste em arremessar um objeto na direção das circunferências e, ao acertá-las, uma pontuação é obtida. Segundo as regras, se um objeto acertar a circunferência maior, o jogador recebe 10 pontos e, acertando a área da figura menor, recebe 10 pontos multiplicados pelo resultado da razão entre a área da circunferência maior e a menor. Nestas condições, qual a pontuação máxima que um jogador pode fazer ao arremessar 5 objetos?
A área de um triângulo com vértices nos pontos A(2,−6),B(2,2) e C(8,−6) é:
Dados os planos x + 2y – 2z + 1 =0 e 2x + 4y - 4z + 4 = 0, calcule a distância entre eles para um ponto (1,1,2) situado no primeiro plano.
Dados os pontos A(2; 3) e B(0; –2). A equação da reta que passa pelos pontos A e B é:
O número máximo possível de pontos de interseção entre uma reta e uma cônica é

