Julgue o item subsequente, relativos às funções f(x) = 30 ! log2(x) e g(x) = 7x ! 2xcos(πx).
A função g(x) é crescente e g(3) < 25.
Considere que uma função 
f(x), para quaisquer x e p reais. A afirmativa correta é
O número de Euler, nome dado em homenagem ao matemático suíço Leonhard Euler, é um número irracional denotado por e, cuja representação decimal tem seus 4 primeiros algarismos dados por 2,718. Esse número é a base dos logaritmos naturais, cuja função f(x) = lnx = logex tem inúmeras aplicações científicas.
A respeito desse assunto, julgue o item a seguir.
A função exponencial g(x) = ex , função inversa de ln x, é uma função crescente.
Cada j = 0, 1, …, 11 representa um mês do ano de 2017, isto é, j = 0 = janeiro, j = 1 = fevereiro, e assim sucessivamente. Se o mês j tem d dias, então j + 1/d representa o dia 1.º do mês j; j + 2/d representa o dia 2 do mês j, e assim sucessivamente, j + d/d = j + 1 representa o dia d do mês j. Dessa forma, cada dia do ano de 2017 pode ser representado por um número x do intervalo [0, 12]. Considere que, nessa representação, em cada dia x do ano de 2017, a porcentagem de água acumulada em relação à capacidade máxima do reservatório de determinada represa seja expressa pelo valor da função f(x) = x2 - 10x + 60.
A partir dessas informações, julgue o item que se segue.
A inversa de
f(x) é expressa por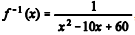 
, para 0 ≤ x ≤ 12.
Qual das opções melhor define uma Função Injetora.
Dada a seguinte função: f(x) = (ax + 3), qual o valor de a para que se tenha f(4) = 27
Dado o dobro de seu cubo somado com o seu quadrado é representado por uma função f(x), com isso, quando x igual a 9, f(x) é igual a:
A circunferência não é a única curva plana localizada na superfície de um cone. Há outras três que foram apresentadas no primeiro trabalho significativo produzido por Apolônio (262-192 a.C.), as quais ele denominou de parábola, hipérbole e elipse (curvas ou seções cônicas). Muitos séculos após, com o surgimento da Geometria Analítica, foi estabelecida toda a base para a representação das curvas cônicas por equações quadráticas. Verificando as equações seguintes:
x2 – 4x + 2y = 0; x2 + y2 - x – y + 1 = 0; 16x2 + 9y2 – 144 = 0; 4x2 + y2 - 8x - 2y + 1 = 0; 4x2 – y2 – 8x + 2y + 7 =0 e x2 + xy + y – 1 = 0.
Identificando as curvas por elas representadas verifica-se que temos n curvas cônicas (elipse, hipérbole, parábola, circunferência). Assim, pode-se afirmar corretamente que
Sobre as funções f: R – {m} → R e g : R – {p} → R – {q} é correto afirmar que
Dada a função f(x – 1) = x2 + 3x – 2, considerando os valores de f(1) e f(2), pode-se afirmar corretamente que
Considere a inequação x2 - 1 ≤ 3 . Está contido no conjunto solução dessa inequação o intervalo
Considerando a função afim f de R em R dada por f(x)=3x-7 , podemos afirmar que:
Quais as raízes da função F(x )=x3-3x2-10x?
Seja a equação geral da reta ax + by + c = 0. Quando a = 0, b ≠ 0 e c ≠ 0, a reta
Sabendo que (x — 5)x + 4 = (x — 1)2 + 3, o valor de x na equação é:
