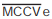Uma churrascaria cobra, no almoço, R$ 12,00 por
pessoa. Após às 15 h, esse valor cai para R$ 9,00. Estimase
que o custo total de um almoço seja de R$ 7,00 por
pessoa. Em média, por dia, almoçam na churrascaria
1 000 clientes, sendo que deles comparecem até às 15 h.
Qual o lucro médio, por dia, da churrascaria?
O sistema de numeração romana, hoje em desuso, já foi o principal sistema de numeração da Europa. Nos dias atuais, a numeração romana é usada no nosso cotidiano essencialmente para designar os séculos, mas já foi necessário fazer contas e descrever números bastante grandes nesse sistema de numeração. Para isto, os romanos colocavam um traço sobre o número para representar que esse número deveria ser multiplicado por 1 000. Por exemplo, o número 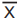
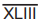
O apresentador de um programa de auditório propôs
aos participantes de uma competição a seguinte tarefa:
cada participante teria 10 minutos para recolher moedas
douradas colocadas aleatoriamente em um terreno
destinado à realização da competição. A pontuação dos
competidores seria calculada ao final do tempo destinado
a cada um dos participantes, no qual as moedas coletadas
por eles seriam contadas e a pontuação de cada um
seria calculada, subtraindo do número de moedas
coletadas uma porcentagem de valor igual ao número
de moedas coletadas. Dessa forma, um participante que
coletasse 60 moedas teria sua pontuação calculada da
seguinte forma: pontuação = 60 − 36 (60% de 60) = 24.
O vencedor da prova seria o participante que alcançasse
a maior pontuação.
Qual será o limite máximo de pontos que um competidor
pode alcançar nessa prova?
Um jovem lança uma bola de borracha para observar
sua trajetória e altura h (em metros) atingida ao longo
de um certo intervalo de tempo t (em segundos). Nesse
intervalo, a bola quica no chão algumas vezes, perdendo
altura progressivamente. Parte de sua trajetória está
descrita na figura a seguir.
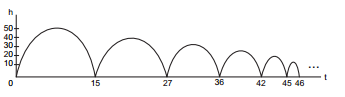
Em suas observações, quantas vezes o jovem pôde
constatar que a bola atingiu a marca de 35 metros?
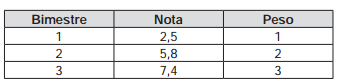
Uma aluna registrou as notas de matemática obtidas
nos 3 primeiros bimestres do ano letivo e seus respectivos
pesos no quadro a seguir.
Ela ainda não sabe qual será sua nota de matemática
no quarto bimestre, mas sabe que o peso dessa nota na
média final é 4. As notas variam de zero a dez, sendo
permitida apenas uma casa na parte decimal (caso
contrário a nota será arredondada, usando como critério “se
o algarismo da segunda casa decimal é maior ou igual a 5,
então o algarismo na primeira casa decimal será acrescido
de uma unidade"). A média final mínima para aprovação na
escola dessa aluna é 7. Se ela obtiver média final inferior
a 7, precisará realizar uma outra prova que substitua a
menor das notas bimestrais, de modo a alcançar a média 7
(mantidos os mesmos pesos anteriores).
Se essa aluna precisar realizar uma prova para substituir
a nota que obteve no primeiro bimestre, e tal nota precisar
ser igual a 4,8, é porque a nota que ela obteve no quarto
bimestre foi
O governo de um país criou o Fundo da Soja e do
Milho, que tem como expectativa inicial arrecadar, por
ano, R$ 36,14 milhões para investimento em pesquisas
relacionadas aos principais produtos da agricultura.
Com isso, a cada operação de venda, seriam destinados
ao Fundo R$ 0,28 por tonelada de soja e R$ 0,22 por
tonelada de milho comercializadas. Para este ano,
espera–se que as quantidades de toneladas produzidas,
de soja e de milho, juntas, seja 150,5 milhões.
Foi pedido a cinco funcionários do Fundo, André, Bruno,
Caio, Douglas e Eduardo, que apresentassem um sistema
que modelasse os dados apresentados. Cada funcionário
apresentou um sistema diferente, considerando x e y como as
quantidades de toneladas comercializadas, respectivamente,
de soja e de milho. O resultado foi o seguinte:

O funcionário que fez a modelagem correta foi
Uma maneira muito útil de se criar belas figuras
decorativas utilizando a matemática é pelo processo
de autossemelhança, uma forma de se criar fractais.
Informalmente, dizemos que uma figura é autossemelhante
se partes dessa figura são semelhantes à figura vista como
um todo. Um exemplo clássico é o Carpete de Sierpinski,
criado por um processo recursivo, descrito a seguir:
• Passo 1: Considere um quadrado dividido em
nove quadrados idênticos (Figura 1). Inicia–se o
processo removendo o quadrado central, restando
8 quadrados pretos (Figura 2).
• Passo 2: Repete–se o processo com cada um dos
quadrados restantes, ou seja, divide–se cada um
deles em 9 quadrados idênticos e remove–se o
quadrado central de cada um, restando apenas os
quadrados pretos (Figura 3).
• Passo 3: Repete–se o passo 2.

Admita que esse processo seja executado 3 vezes, ou
seja, divide–se cada um dos quadrados pretos da Figura
3 em 9 quadrados idênticos e remove–se o quadrado
central de cada um deles.
O número de quadrados pretos restantes nesse momento é
Parece que foi ontem. Há 4,57 bilhões de anos,
uma gigantesca nuvem de partículas entrou em colapso
e formou o nosso Sistema Solar. Demoraram míseros
28 milhões de anos — um piscar de olhos em termos
geológicos — para que a Terra surgisse. Isso aconteceu
há 4,54 bilhões de anos. No começo, a superfície do
planeta era mole e muito quente, da ordem de 1 200 °C.
Não demorou tanto assim para a crosta ficar mais fria e
surgirem os mares e a terra; isso aconteceu há 4,2 bilhões
de anos. História da Terra. Superinteressante, nov. 2011 (adaptado).
O nosso Sistema Solar se formou, em anos, há
Um maquinista de trem ganha R$ 100,00 por viagem e só pode viajar a cada 4 dias. Ele ganha somente se fizer a viagem e sabe que estará de férias de 1o a 10 de junho, quando não poderá viajar. Sua primeira viagem ocorreu no dia primeiro de janeiro. Considere que o ano tem 365 dias.
Se o maquinista quiser ganhar o máximo possível, quantas viagens precisará fazer?
Nos shopping centers costumam existir parques com vários brinquedos e jogos. Os usuários colocam créditos em um cartão, que são descontados por cada período de tempo de uso dos jogos. Dependendo da pontuação da criança no jogo, ela recebe um certo número de tíquetes para trocar por produtos nas lojas dos parques.
Suponha que o período de uso de um brinquedo em certo shopping custa R$ 3,00 e que uma bicicleta custa 9.200 tíquetes.
Para uma criança que recebe 20 tíquetes por período de tempo que joga, o valor, em reais, gasto com créditos para obter a quantidade de tíquetes para trocar pela bicicleta é
Maria quer inovar em sua loja de embalagens e decidiu vender caixas com diferentes formatos. Nas imagens apresentadas estão as planificações dessas caixas.
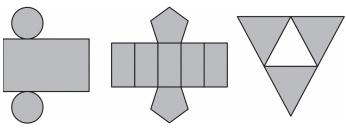
Quais serão os sólidos geométricos que Maria obterá a partir dessas planificações?
João decidiu contratar os serviços de uma empresa por telefone através do SAC (Serviço de Atendimento ao Consumidor). O atendente ditou para João o número de protocolo de atendimento da ligação e pediu que ele anotasse. Entretanto, João não entendeu um dos algarismos ditados pelo atendente e anotou o número 1 3 _ 9 8 2 0 7, sendo que o espaço vazio é o do algarismo que João não entendeu.
De acordo com essas informações, a posição ocupada pelo algarismo que falta no número de protocolo é a de
A tabela a seguir mostra a evolução da receita bruta anual nos três últimos anos de cinco microempresas (ME) que se encontram à venda.
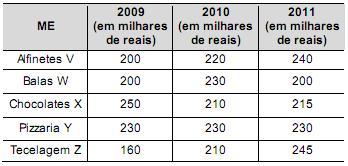
Um investidor deseja comprar duas das empresas listadas na tabela. Para tal, ele calcula a média da receita bruta anual dos últimos três anos (de 2009 até 2011) e escolhe as duas empresas de maior média anual.
As empresas que este investidor escolhe comprar são
Um forro retangular de tecido traz em sua etiqueta a informação de que encolherá após a primeira lavagem mantendo, entretanto, seu formato. A figura a seguir mostra as medidas originais do forro e o tamanho do encolhimento (x) no comprimento e (y) na largura. A expressão algébrica que representa a área do forro após ser lavado é (5 x) (3 y).
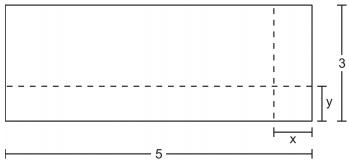
Nestas condições, a área perdida do forro, após a primeira lavagem, será expressa por
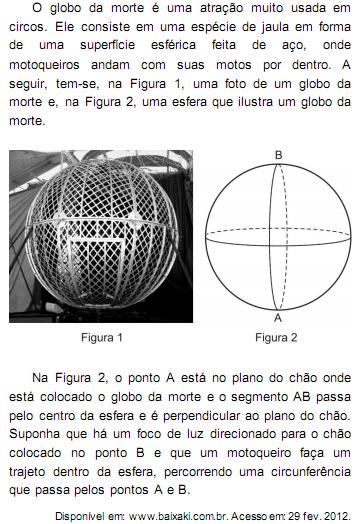
A imagem do trajeto feito pelo motoqueiro no plano do chão é melhor representada por