Se o percentil de 5% superior da distribuição quiquadrado com 2 graus de liberdade for igual a 5,99, então é correto inferir que há fraca evidência amostral para assumir que as proporções amostrais observadas diferem das proporções verificadas.
Em um estudo oncológico, foi registrado o tempo, em semanas, de sobrevida de pacientes com leucemia aguda. Na data do diagnóstico da patologia, registrou-se também o número de glóbulos brancos, em escala logarítmica. Por meio de uma análise exploratória de dados, assumiu-se que os tempos de sobrevida ti, i = 1, ..., n, em que n é o tamanho da amostra, seguem distribuição exponencial. A tabela a seguir apresenta medidas-resumo, calculadas por meio de um software estatístico, na qual o tempo de sobrevida dos pacientes está em unidade de tempo apropriada, e o número de glóbulos brancos está em logaritmo neperiano (ln).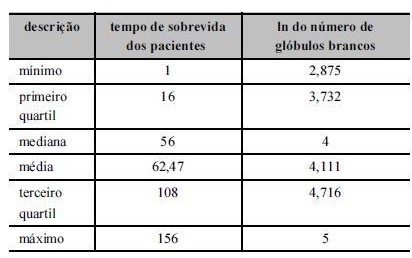
A partir dessas informações, julgue os itens a seguir.
A função densidade de probabilidade para a distribuição exponencial, utilizando estatísticas calculadas sobre a amostra, pode ser expressa por 
com esperança matemática E(T) = 62,47.
A probabilidade de um paciente sobreviver mais de 30 semanas, considerando que ele se encontra vivo há mais de 10 semanas da data do diagnóstico, é igual à probabilidade de o mesmo paciente sobreviver mais de 20 semanas.
No modelo de regressão múltipla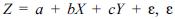 
representa um desvio aleatório. Com referência a esse modelo, julgue os próximos itens.
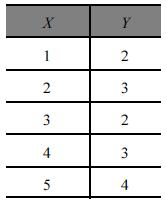
Considerando a tabela de valores acima, nas variáveis X e Y, julgue os itens subsequentes.
Se Cov (X, Y) é a covariância entre X e Y, V(X) é a varância de X e V(Y) é a variância de Y, então é correto afirmar que o coeficiente de correlação linear, Corr(X, Y) =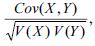 
é inferior a 0,8.
A estimativa para a altura média da população é igual a 169 cm.
Considere que uma pequena população seja composta de 12 pessoas com os seguintes pesos:
75 80 65 90 70 72 60 70 85 65 80 76
Com base nesses dados, julgue os itens que se seguem.
As amostras sistemáticas de tamanho 3 correspondem às colunas do seguinte esquema retangular:
e o peso médio esperado de uma amostra sistemática é de 74 kg.
No último mês, Alípio fez apenas 8 ligações de seu telefone celular cujas durações, em minutos, estão apresentadas no rol abaixo.
5 2 11 8 3 8 7 4
O valor aproximado do desvio padrão desse conjunto de tempos, em minutos, é
Para comparar os lucros de dois grupos de empresas, I e II, foram preparados desenhos esquemáticos com os valores observados dos lucros, em milhões de reais, representados abaixo.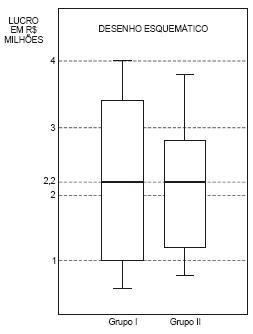
Analisando estes diagramas, observa-se que
Uma amostra aleatória com 16 elementos é extraída de uma população normal de tamanho infinito com média ? e desvio padrão desconhecido. O valor da média amostral e o valor da variância amostral foram iguais a M e 625, respectivamente. Deseja-se testar a hipótese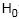 
: ? = 90 (hipótese nula) contra 
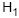: ? > 90 (hipótese alternativa) com base nos resultados apresentados pela amostra, ao nível de significância de 5%. Utilizou-se para o teste a distribuição t de Student, considerando
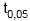o quantil da distribuição t de Student para o teste unicaudal tal que P (t > 
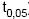) = 5%.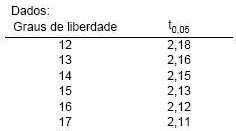
Sabendo-se que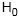 
não foi rejeitada, então o valor de M foi, no máximo,
Em um modelo de regressão linear múltipla com heteroscedasticidade, aplicou-se o método dos mínimos quadrados generalizados. É correto afirmar, com relação ao modelo original, isto é, antes da aplicação deste método, queEm um modelo de regressão linear múltipla com heteroscedasticidade, aplicou-se o método dos mínimos quadrados generalizados. É correto afirmar, com relação ao modelo original, isto é, antes da aplicação deste método, que
Em uma população suponha que:
? 80% dos adultos do sexo masculino sejam alfabetizados;
? 60% dos adultos do sexo feminino sejam alfabetizados.
A proporção de adultos do sexo masculino e feminino é igual.
Sorteando-se ao acaso e com reposição uma amostra de 3 pessoas desta população, a probabilidade de se encontrar pelo menos uma alfabetizada na amostra é
A demanda diária por um produto e uma variável aleatória X , contínua, com função densidade de probabilidade dada por
A média e a mediana de X são dadas, respectivamente, por
Sejam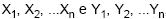 
, ...Yn, duas amostras aleatórias independentes, extraídas, cada uma delas com reposição, de duas distribuições uniformes contínuas com parâmetros [
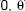] e [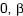
], respectivamente. Nestas condições, a média e a variância da variável aleatória 
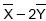, onde 
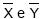são as respectivas médias amostrais das duas amostras citadas, são dadas respectivamente por:
O histograma que melhor representa, em um estudo de uma pequena cidade, a variável altura de uma família em que os pais têm menos de 24 anos é
