Seja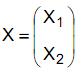 
um vetor de variáveis aleatórias e seja = ? 
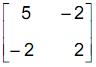sua matriz de covariâncias. Seja Y a segunda componente principal da matriz ?. A proporção da variância total de X que é explicada por Y é
Um pesquisador pretende verificar se duas amostras aleatórias extraídas, independentemente, de uma grande população, referente aos salários de uma categoria profissional, diferem quanto ao seu valor mediano. O tamanho de cada amostra é igual a 25 e a mediana do conjunto de valores das amostras reunidas é igual à média aritmética entre o 25º e 26º elementos, com os valores do conjunto em ordem crescente. A tabela abaixo demonstra a comparação dos valores das amostras com relação ao valor dessa mediana.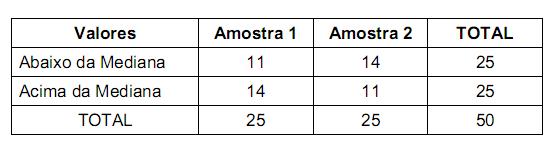 
O pesquisador utilizou o teste da mediana para decidir se as medianas das duas amostras são iguais, ao nível de significância de 5%. As hipóteses formuladas foram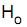 
: As medianas são iguais (hipótese nula) e 
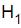: As medianas são diferentes (hipótese alternativa), sabendo que ao nível de significância de 5% a variável qui-quadrado com 1 grau de liberdade é igual a 3,84. Então, uma conclusão correta é que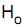 
A função procura de um determinado produto é dada por y =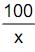 
, (x > 0), e a função oferta é dada por y = 25 x. Observação: y corresponde à quantidade produzida e vendida do produto, sendo x o respectivo preço unitário de venda. Se 
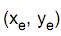é o ponto de encontro da função procura e da função oferta (ponto de equilíbrio do mercado), então a equação da reta tangente à curva y = 
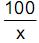no ponto 
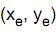é dada por
A população correspondente aos salários dos empregados de um determinado ramo de atividade é considerada normal, de tamanho infinito e desvio padrão populacional igual a R$ 400,00. Uma amostra aleatória de tamanho 100 é extraída desta população obtendo-se uma média igual a R$ 2.050,00. Com base nesta amostra, deseja-se testar a hipótese se a média µ da população é igual a R$ 2.000,00, a um nível de significância de 5%. Foram formuladas as hipóteses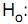 
µ = R$ 2.000,00 (hipótese nula) e 
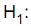µ ? R$ 2.000,00 (hipótese alternativa). Para a tomada de decisão, o valor do escore reduzido, utilizado para comparação com o valor z da distribuição normal padrão (Z) tal que a probabilidade P (|Z| > z) = 5%, é
Em um setor de um órgão público, verificou-se a existência de 6 valores de salário entre seus 32 funcionários. A tabela abaixo fornece a quantidade de funcionários que recebe cada valor de salário, em que (3X - 2Y) = 0. 
Com relação aos valores destes salários, a soma da média aritmética com a mediana e com a moda é igual a
Considere que a quantidade de processos que chegam a um
auditor diariamente siga uma distribuição de Poisson, com
parâmetro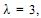 
e que cada processo, independentemente dos
demais, tenha probabilidade 0,2 de incorrer em algum tipo de
irregularidade. Com base nessa situação, julgue os itens que se
seguem.
Caso o auditor seja capaz de avaliar, no máximo, quatro processos por dia, então, o número esperado de processos avaliados por ele será inferior a três.
Considere uma amostra aleatória de tamanho 4: (X, Y, Z, T) extraída de uma população normal de média µ e variância unitária. A classe de estimadores E = (K - 2) X - KY + (2 - K) Z + (K + 1) T é utilizada para estimar a média µ da população, sendo K um parâmetro real. Entre os estimadores desta classe, o mais eficiente apresenta uma variância igual a
Em um período de 200 dias úteis, observou-se em uma repartição pública a autuação de processos apresentando uma certa característica. A fórmula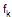 
= 10 + 45 K - 10 K2 fornece a informação do número de dias úteis 
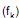em que se verificou a autuação de K destes processos, sendo que K assume somente os valores 0, 1, 2, 3 e 4. Calculando, para o período considerado, os respectivos valores da média aritmética (quantidade de processos autuados por dia), da mediana e da moda, a soma destes 3 valores é
Considere as afirmativas abaixo.
I. Sabe-se que a variável aleatória contínua Z é a soma de k variáveis aleatórias independentes, todas com distribuição N (0, 1). Nessas condições Z tem distribuição qui-quadrado com k graus de liberdade.
II. Sabe-se que Y é uma variável aleatória com distribuição Gama com parâmetros a = 1 e ß = 0. Se ß = 2, e a = k/2, então Y tem distribuição qui-quadrado com k graus de liberdade.
III. Sabe-se que Z é uma variável aleatória N (0, 1) e que Y é uma qui-quadrado com 1 grau de liberdade. Nessas condições, a variável aleatória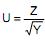 
tem distribuição t de Student com 1 grau de liberdade.
Está correto o que se afirma APENAS em
As questões de números 64 a 67 referem-se em informações dadas abaixo.
Se Z tem distribuição normal padrão, então:
P (Z < 0,28) = 0,61; P (Z < 1,28) = 0,9; P (Z < 1,5) = 0,933; P (Z < 1,96) = 0,975; P (Z < 2) = 0,977.
A proporção p dos funcionários do sexo feminino de um órgão público é de 20%. Colheu-se uma amostra aleatória simples (AAS) com reposição de 64 funcionários desse órgão e calculou-se a proporção amostral,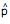 
, de funcionários do sexo feminino na amostra. Fazendo-se uso da aproximação pela normal para a distribuição de 
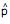, a probabilidade de que essa proporção difira de p em menos do que 10% é
A função geradora de momentos de uma variável aleatória X é dada por: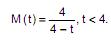 
Nessas condições, a média e a variância da variável aleatória Y = 2X + 1 são dadas, respectivamente, por
Uma urna contém 4 bolas numeradas de 1 a 4. Duas bolas são retiradas, sucessivamente, ao acaso e sem reposição. Seja X a variável aleatória definida por:
X =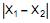 
, onde 
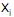= número obtido na i-ésima bola retirada, i = 1,2.
Nessas condições, a probabilidade de X ser maior ou igual a 2 é
Um setor de um órgão público é composto por 80 funcionários, sendo 40 homens e 40 mulheres. Três tipos de processos (M, N e P) são analisados pelos funcionários deste setor. Uma pesquisa é realizada com todos estes funcionários perguntando qual tipo de processo prefere analisar. Cada um deu uma e somente uma resposta entre as opções M, N e P resultando no seguinte quadro: 
Utilizou-se o teste qui-quadrado para concluir se a preferência pelos tipos de processos depende do sexo.
Dados: Valores críticos da distribuição qui-quadrado [P (qui-quadrado com n graus de liberdade < valor tabelado) = (1 - a)] 
Pode-se afirmar que uma conclusão correta é que
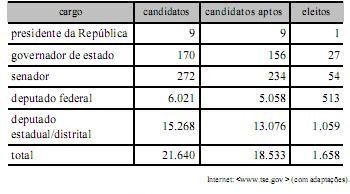
Com base na tabela acima, referente às eleições de 2010, que apresenta a quantidade de candidatos para os cargos de presidente da República, governador de estado, senador, deputado federal e deputado estadual/distrital, bem como a quantidade de candidatos considerados aptos pela justiça eleitoral e o total de eleitos para cada cargo pretendido, julgue os itens a seguir.
A variável cargo classifica-se como uma variável qualitativa ordinal.
