A variável aleatória X tem distribuição binomial com média 10 e variância 9. A variável aleatória Y tem distribuição binomial com variância igual a 16 e cuja probabilidade de sucesso é o dobro da probabilidade de sucesso da variável aleatória X. Fazendo uso da aproximação à distribuição normal, sem fazer a correção de continuidade, a probabilidade de Y ser superior a 27 é
Se a função geratriz de momentos da variável aleatória X é dada por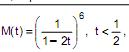 
então a média da variável aleatória Y = 0,5X - 6 é igual a
As probabilidades de um contador, A, demorar uma, duas ou três horas para preencher uma declaração de imposto de renda são dadas, respectivamente, por 1 ⁄ 4 e 1 ⁄ 2 , 1 ⁄ 4 . Dentre 5 declarações escolhidas aleatoriamente e com reposição, das declarações que A deverá elaborar, a probabilidade dele demorar para o preenchimento, em três delas 1 hora, em uma 2 horas e na restante 3 horas, é igual a
Todos os funcionários de 5 grupos de trabalho com 6 funcionários cada um, escolhidos aleatoriamente, são designados para realizar uma tarefa, independentemente. O tempo que cada um dos 30 funcionários levou para concluir a tarefa é anotado. Deseja-se saber, a um determinado nível de significância, se os tempos médios dos grupos para a realização da tarefa são iguais. Considere algumas informações do quadro de análise de variância: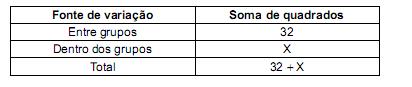 
Se o valor da estatística F (F calculado) utilizado para testar a igualdade dos tempos médios apresentou um valor igual a 20, então X é igual a
O tamanho de uma população normalmente distribuída, com um desvio padrão populacional igual a 128, é igual a 1025. Uma amostra aleatória de tamanho 64 é extraída, sem reposição, desta população. Com base nesta amostra e considerando que na distribuição normal padrão (Z) a probabilidade P(Z > 1,96) = 0,025, obteve-se um intervalo de confiança de 95% com uma amplitude igual a
Em um censo realizado em uma empresa, verificou-se que a média aritmética dos salários de seus empregados foi igual a R$ 2.000,00 com um desvio padrão igual a R$ 125,00. Analisando, separadamente, o grupo de todos os empregados do sexo masculino e o grupo de todos os empregados do sexo feminino obteve-se as seguintes informações: 
A porcentagem de empregados do sexo masculino na empresa é de
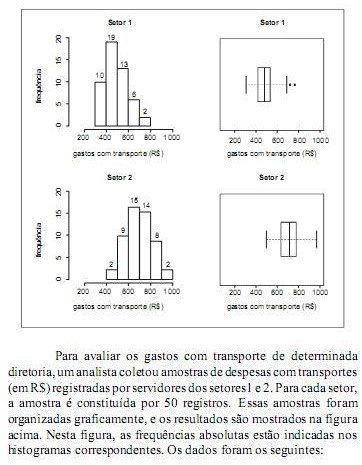
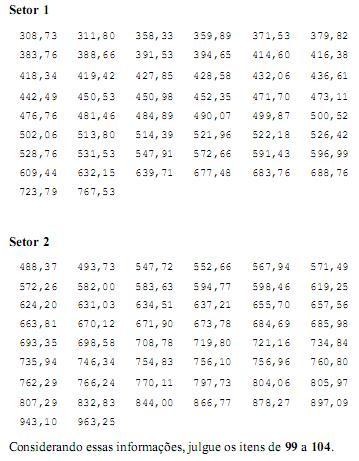
A despesa média com transporte dos servidores do setor 1 é superior a R$ 500,00.
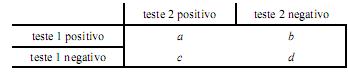
Com relação ao teste de McNemar aplicado à tabela de contingência acima, assinale a opção correta.
Os estimadores ?n e ?*n são estimadores pontuais do parâmetro ? de certa distribuição, em que n representa o tamanho da amostra. Nesse caso, o estimador ?
Considerando que x1, x2, ..., xn seja uma amostra aleatória e que X seja a média aritmética dessa amostra, é correto afirmar que F = 1/n Sni =1 (xi - X)
Na série temporal {X(t)}, deseja-se efetuar o teste de hipóteses: H0 : X(t) = X(t 1) + a(t) versus HA : X(t) = Φ X(t 1) + a(t), em que Φ é tal que |Φ| < 1 e a(t) representa o choque aleatório. Nesse caso, o teste apropriado para essa situação é o teste
Um analista efetuou uma pesquisa sobre o perfil do menor infrator. Para cada menor observado na amostra, foram observadas 15 medidas supostamente gaussianas. O analista deseja classificar as unidades amostrais em grupos, de modo que as pessoas que pertencem a um mesmo grupo tenham, estatisticamente, um tipo de similaridade com base nas 15 medidas consideradas. Com base nessas informações, é correto afirmar que a técnica multivariada apropriada para a finalidade desejada pelo analista é a análise
Neste estudo, a teoria de filas foi empregada para descrever as filas que se formam nos caixas de certo supermercado. O interesse particular desse estudo é a determinação do tempo médio que cada cliente gasta em espera na fila. Dois modelos foram considerados: (i) sistema M/M/m em fila única e (ii) sistema M/M/1 em m filas paralelas e independentes.
R. Morabito e F. C. R. de Lima. Um modelo para analisar o problema de filas em caixas de supermercados: um estudo de caso. Pesquisa Operacional, vol. 20, n.º 1, jun./2000, p. 59-71 (com adaptações).
Com relação ao assunto abordado no texto acima, assinale a opção correta.
Um analista estudou o pagamento dos valores Y (em R$ mil) das custas processuais em ações trabalhistas. Com base em uma amostra aleatória simples de processos judiciais, ele concluiu que a variável Y se relaciona linearmente com o valor da causa X (em R$ mil), conforme uma reta ajustada pelo método de mínimos quadrados ordinários na forma Y = 0,1 × X + 200. A média populacional e a amostral da variável X foram, respectivamente, iguais a R$ 100 mil e R$ 90 mil.
Nesse caso, é correto afirmar que a estimativa de regressão para a média populacional de Y foi igual a
