Os volumes com que são preenchidos os frascos de perfume produzidos por certa marca são normalmente distribuídos com média 100 mL e desvio padrão de 2 mL. Frascos que apresentam menos de 95 mL ou mais de 105 mL de perfume são considerados fora dos limites e inadequados pelo controle de qualidade.
A porcentagem de frascos produzidos com volume considerado inadequado é igual a
Suponha uma amostra aleatória simples de tamanho 2 de uma densidade exponencial com parâmetro λ > 0, e seja Y a menor das observações.
Nesse caso, Y tem distribuição
Se a variável aleatória U tem distribuição qui-quadrado com 4 graus de liberdade e a variável aleatória Z tem distribuição N(0,1), U e Z independentes, então a variável aleatória W = U/Z2 tem distribuição
Avalie se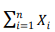 
é uma estatística suficiente para o parâmetro indicado nos casos a seguir.
I. Uma distribuição Bernoulli para a qual o parâmetro p (0 < p <1) é desconhecido.
II. Uma distribuição geométrica para a qual o parâmetro p (0 < p < 1) é desconhecido.
III. Uma distribuição normal com média conhecida e variância σ2 desconhecida.
Está correto o que se afirma em
Acerca da amostragem estratificada, analise as afirmativas a seguir.
I. Visa a produzir estimativas mais precisas, produzir estimativas para a população toda e para subpopulações.
II. Em geral, quanto menos os elementos de cada estrato forem parecidos entre si e também entre os estratos, maior será a precisão dos estimadores.
III. A estratificação produz necessariamente estimativas mais eficientes do que a amostragem aleatória simples.
Está correto o que se afirma em
Se b0 e b1 são as estimativas por mínimos quadrados de β0 e β1, respectivamente, então seus valores são dados por
Suponha que, para se fazer inferências acerca de uma proporção populacional θ, 0 < θ < 1, uma amostra aleatória simples x1, x2, .., xn, de tamanho n de uma distribuição Bernoulli (θ) deva ser observada; suponha, ainda, que se pretenda usar uma densidade Uniforme no intervalo (0, 1) a priori para θ.
Assim, se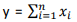 
, então a função de densidade a posteriori para θ terá distribuição Beta com parâmetros
As equações x2 -4x + 3 = 0 e x2 + x +m = 0 tem uma raiz em comum.
A soma dos possíveis valores de m é
Considere as funções reais definidas por f(x)=3x+1 e g(x)=2x+b , sendo b real.
Se g(f(2)) = 0, então f(g(2)) é igual a
Considere a reta r de equação 2x + 3y + 7 = 0 e a reta s, perpendicular à reta r e que passa pelo ponto (1, 3).
A interseção da reta s com o eixo X é
Uma moeda é lançada quatro vezes. A probabilidade de saírem mais caras do que coroas é de
Sabe-se que sen x - cos x = 0,6 .
O valor de y = sen x ∙ cos x é
O plano cartesiano representado a seguir está quadriculado e cada quadrícula tem lado de 1 unidade.
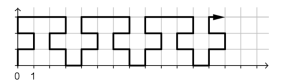
Uma linha poligonal foi desenhada mantendo sempre a repetição de determinado padrão.
Um percurso sobre essa poligonal, começando no ponto (0, 0) e com 2018 unidades de comprimento, terá sua extremidade no ponto
O valor de y = cos 36° . cos 72° é
Um barril com a forma de um cilindro circular reto com 60 cm de diâmetro e 1 m de altura tem, aproximadamente, a capacidade de
