O Sr. Ramoile, professor de Estatística aposentado, vem há muito tempo acompanhando os dados sobre custos e faturamento do restaurante de sua filha Cecília. O restaurante funciona todos os dias da semana e o Sr. Ramoile concluiu que: o custo diário do restaurante segue uma distribuição normal, com média igual a R$ 500,00 e desvio- padrão igual a R$ 10,00 e que o faturamento diário, também, apresenta uma distribuição normal, com média R$ 800 e desvio-padrão R$ 20. Como o Sr. Ramoile conhece muito bem os princípios básicos da estatística, ele sabe que, se uma variável Z seguir uma distribuição normal padrão, então Z tem média 0 e variância 1. Ele também sabe que a probabilidade dessa variável Z assumir valores no intervalo entre 0 < Z < 2 - ou seja, entre a média 0 e 2 desvios-padrão - é, aproximadamente, igual a 0,4772. Cecília, muito preocupada com o futuro de seu restaurante, perguntou a seu pai se ele poderia verificar a probabilidade de, em um dia qualquer, o custo ser maior do que R$ 520,00 e o faturamente ficar no intervalo entre R$ 760,00 e R$ 840,00. Após alguns minutos, o Sr. Ramoile disse, acertadamente, que as respectivas probabilidades são, em termos percentuais, iguais a
Em um órgão público, 40 relatórios de prestação de contas
que apresentaram erro serão novamente analisados e, para que esse
trabalho seja executado mais eficientemente, esses relatórios foram
separados em dois grupos (A e B), cada um com 20 relatórios. Em
cada grupo, os relatórios foram classificados, de acordo com o erro
apresentado, em EM = relatório com erro de natureza média;
EG = relatório com erro de natureza grave; ou EGS = relatório com
erro de natureza gravíssima. Escolhendo-se, aleatoriamente, um
relatório do grupo A, sabe-se que as probabilidades de ele ser
classificado como EM, EG ou EGS são, respectivamente:
PA(EM) = 0,5; PA(EG) = 0,3; PA(EGS) = 0,2. No caso de relatório
do grupo B, as probabilidades são: PB(EM) = 0,1; PB(EG) = 0,6;
PB(EGS) = 0,3.
A probabilidade de se escolher, aleatoriamente, três relatórios,
sendo dois do grupo A e um do grupo B, todos classificados
como EGS, é expressa por (4/20) × (3/19) × (6/20).
Em um jogo disputado em uma mesa de sinuca, há 16 bolas: 1 branca e 15 coloridas, as quais, de acordo com a coloração, valem de 1 a 15 pontos (um valor para cada bola colorida).
O jogador acerta o taco na bola branca de forma que esta acerte as outras, com o objetivo de acertar duas das quinze bolas em quaisquer caçapas. Os valores dessas duas bolas são somados e devem resultar em um valor escolhido pelo jogador antes do início da jogada.
Arthur, Bernardo e Caio escolhem os números 12, 17 e 22 como sendo resultados de suas respectivas somas.
Com essa escolha, quem tem a maior probabilidade de ganhar o jogo é
José e Antônio discutiam qual dos dois teria mais chances de acertar na loteria. José tinha gasto R$ 14,00 numa aposta de 7 números na Mega-Sena, enquanto Antônio gastou R$ 15,00 em três apostas da quina, não repetindo números em suas apostas. Na discussão, eles consideravam a chance de José acertar a quadra da Mega-Sena e de Antônio acertar o terno da Quina.
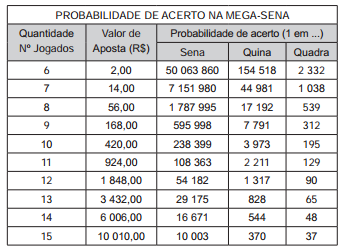
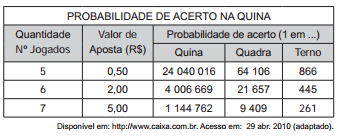
Nessas condições, a razão entre as probabilidades de acerto de José e de Antônio nos menores prêmios de cada loteria é
Atenção: Para resolver às questões de números 52 e 53, considere os dados abaixo:
A empresa de aviação T tem 4 balcões de atendimento ao público: A, B, C e D. Sabe-se que, num determinado dia, os balcões A e B atenderam, cada um, a 20%; C e D atenderam, cada um, a 30% do público que procurou atendimento em T. Sabe-se ainda que A, B, C e D atenderam, respectivamente, 5%, 15%, 10% e 20% de pessoas com atendimento prioritário (idosos, deficientes, gestantes ou mães com crianças no colo, etc).
Selecionando-se ao acaso e com reposição cinco pessoas atendidas no balcão D, nesse mesmo dia, a probabilidade de exatamente duas terem sido do grupo de atendimento prioritário é de
Um dado é viciado de tal modo que a probabilidade de ocorrer face par é duas vezes mais provável do que ocorrer face ímpar. O dado é lançado duas vezes independentemente. Considere os seguintes eventos:
A = a soma dos pontos das faces é 6;
B = o número da face do primeiro dado é menor do que 3.
Nessas condições, a probabilidade de A, sabendo que ocorreu B, é
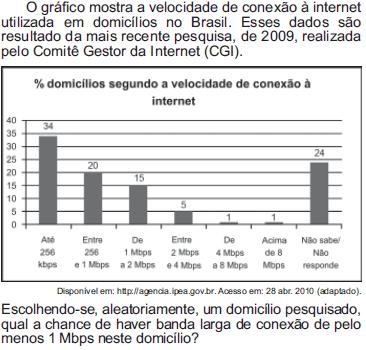
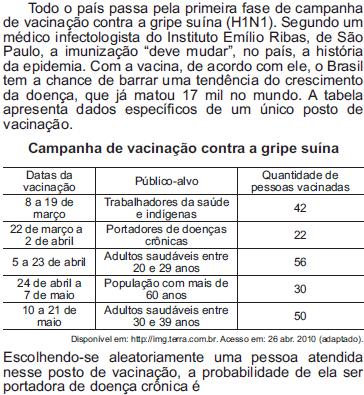
Observe os dados da tabela seguinte, sobre o número de ocorrências de acidente de trabalho no Brasil em 2004
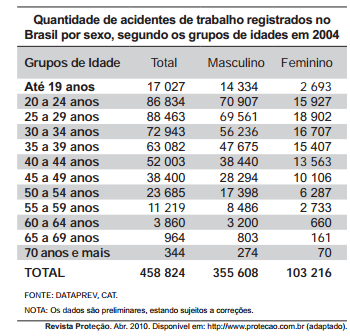
O risco de acidente de trabalho de grupos de estudo é o resultado da probabilidade experimental calculada a partir de dados estatísticos. Assim sendo, considerando o disposto na tabela, qual o risco aproximado de um acidentado ser um homem com idade entre 25 e 29 anos?
Para verificar e analisar o grau de eficiência de um
teste que poderia ajudar no retrocesso de uma doença
numa comunidade, uma equipe de biólogos aplicou–o
em um grupo de 500 ratos, para detectar a presença
dessa doença. Porém, o teste não é totalmente eficaz,
podendo existir ratos saudáveis com resultado positivo
e ratos doentes com resultado negativo. Sabe–se,
ainda, que 100 ratos possuem a doença, 20 ratos são
saudáveis com resultado positivo e 40 ratos são doentes
com resultado negativo.
Um rato foi escolhido ao caso, e verificou–se que seu
resultado deu negativo. A probabilidade de esse rato ser
saudável é

Admita que a probabilidade de uma pessoa de um particular grupo genético ter uma determinada doença é de 30%. Um custoso e invasivo exame para diagnóstico específi co dessa doença tem uma probabilidade de um resultado falso positivo de 10% e de um resultado falso negativo de 30%. Considerando que uma pessoa desse grupo genético com suspeita da doença fez o referido exame, qual a probabilidade dela ter a doença dado que o resultado do exame foi negativo?
Se A e B são eventos independentes com probabilidades P[A] = 0,4 e P[B] = 0,5 então P[A ? B] é igual a:
Os estilos musicais preferidos pelos jovens brasileiros
são o samba, o rock e a MPB. O quadro a seguir registra
o resultado de uma pesquisa relativa à preferência
musical de um grupo de 1 000 alunos de uma escola.
Alguns alunos disseram não ter preferência por nenhum
desses três estilos.
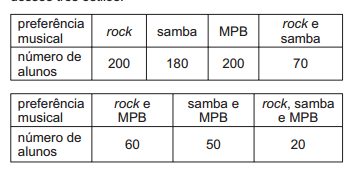
Se for selecionado ao acaso um estudante no grupo
pesquisado, qual é a probabilidade de ele preferir
somente MPB?
Um experimento foi conduzido com o objetivo de avaliar o poder germinativo de duas culturas de cebola, conforme a tabela.
Germinação de sementes de duas culturas de cebola
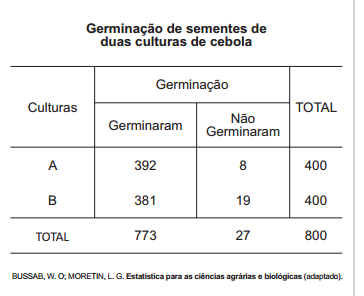
Desejando-se fazer uma avaliação do poder germinativo de uma das culturas de cebola, uma amostra foi retirada ao acaso. Sabendo-se que a amostra escolhida germinou, a probabilidade de essa amostra pertencer Cultura A é de

