Um plano de benefícios adota o modelo bidecremental, em
que os decrementos constituem morte e invalidez. Nesse plano, a
probabilidade de morte aos 51 anos de idade é igual a 0,02 e a
probabilidade de entrada em invalidez aos 51 anos é igual a 0,003.
Com relação ao plano de benefícios mencionado acima, julgue os itens
subseqüentes.
A probabilidade de uma pessoa viva e ativa de 51 anos de idade morrer aos 52 anos de idade corresponde a 0,017.
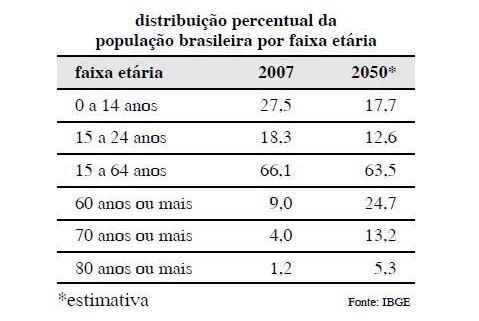
De acordo com dados do IBGE, em 2007, 6,4% da população
brasileira tinha 65 anos de idade ou mais e, em 2050, essa parcela, que
constitui o grupo de idosos, corresponderá a 18,8% da população.
Com base nessas informações e nas apresentadas na tabela acima,
julgue os itens seguintes.
Se, em 2050, três pessoas da população brasileira forem escolhidas ao acaso, a probabilidade de todas elas terem até 59 anos de idade é inferior a 0,4.
A partir do texto acima, julgue os itens subseqüentes, considerando que, para avaliar a tese de que a probabilidade foi reduzida para 0,9p, será efetuada uma nova pesquisa com 900 pessoas selecionadas aleatoriamente entre aquelas que sofreram o primeiro infarto do miocárdio no período de cinco anos antes até cinco anos depois da publicação do veto.
A partir dos resultados da nova pesquisa, considere a realização de um teste de hipóteses cuja hipótese nula (H0 ) seja Pa = Pd , em que Pa e Pd são as probabilidades de uma pessoa sofrer o primeiro infarto do miocárdio, respectivamente, antes e depois da publicação do veto. Nesse caso, das 900 pessoas que compõem a amostra, se a quantidade de pessoas que sofreram o primeiro infarto do miocárdio depois da publicação do veto for igual ou superior a 451, então é correto concluir que a hipótese nula é falsa.
A probabilidade de um indivíduo de idade x sobreviver mais
n anos é representada por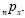 
Considerando a como a idade de
aposentadoria normal em um plano previdenciário, a
probabilidade de um indivíduo de idade x sobreviver até a idade
a é dada por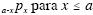 
, e a probabilidade de um indivíduo
de idade y sobreviver além da idade a é dada por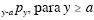 
.
Considerando, ainda, que a é igual a 60 anos de idade, têm-se as
seguintes probabilidades, para x e y dados em anos.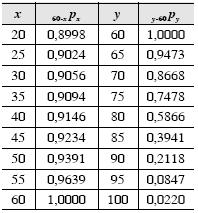
Com base nessas informações, julgue os itens que se seguem.
Na situação em que duas pessoas de uma população, uma com 20 anos de idade, e outra com 50 anos e idade, sejam selecionadas aleatoriamente, a probabilidade de essas duas pessoas sobreviverem até a idade de aposentadoria - 60 anos - é maior que 0,83.
A partir do texto acima, julgue os itens subseqüentes, considerando que, para avaliar a tese de que a probabilidade foi reduzida para 0,9p, será efetuada uma nova pesquisa com 900 pessoas selecionadas aleatoriamente entre aquelas que sofreram o primeiro infarto do miocárdio no período de cinco anos antes até cinco anos depois da publicação do veto.
Caso a tese dos cientistas italianos esteja correta, então, entre o grupo de 900 pessoas que farão parte da nova pesquisa, o número esperado de pessoas que sofreram o primeiro infarto do miocárdio após a publicação do veto é superior a 420 e inferior a 450 pessoas.
Um estudo de L. Y. Wang et al., publicado no Journal
of Adolescent Health, em 2008, estabeleceu uma relação entre
o índice de massa corporal (x) de uma pessoa na adolescência e
a probabilidade de essa pessoa tornar-se obesa quando adulta, por
meio de um modelo de regressão não-linear na forma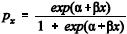
, em que 
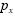representa a probabilidade
esperada de uma pessoa tornar-se obesa na fase adulta, dado que,
na adolescência, a massa corporal era igual a um valor x, e ? e ?
são coeficientes do modelo. Segundo os autores do estudo,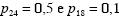
.
Com base nessas informações, julgue os itens de 108 a 110.
Segundo esse estudo, a probabilidade de uma pessoa tornar-se obesa na fase adulta, quando sua massa corporal na adolescência for igual a x, será igual, em média, a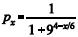
.
A probabilidade de um indivíduo de idade x sobreviver mais
n anos é representada por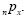 
Considerando a como a idade de
aposentadoria normal em um plano previdenciário, a
probabilidade de um indivíduo de idade x sobreviver até a idade
a é dada por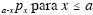 
, e a probabilidade de um indivíduo
de idade y sobreviver além da idade a é dada por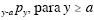 
.
Considerando, ainda, que a é igual a 60 anos de idade, têm-se as
seguintes probabilidades, para x e y dados em anos.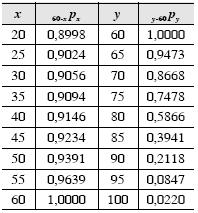
Com base nessas informações, julgue os itens que se seguem.
É esperado que mais de 20% dos indivíduos atualmente com 60 anos de idade alcancem a idade de 90 anos.
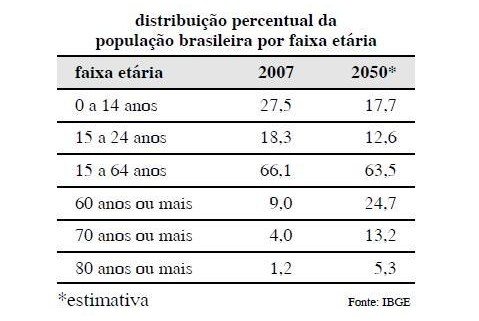
De acordo com dados do IBGE, em 2007, 6,4% da população
brasileira tinha 65 anos de idade ou mais e, em 2050, essa parcela, que
constitui o grupo de idosos, corresponderá a 18,8% da população.
Com base nessas informações e nas apresentadas na tabela acima,
julgue os itens seguintes.
Considere-se que, em 2050, serão aleatoriamente selecionados três indivíduos, um após o outro, do grupo de pessoas que compõem a parcela da população brasileira com 15 anos de idade ou mais. Nessa situação, a probabilidade de que apenas o terceiro indivíduo escolhido tenha pelo menos 65 anos de idade será superior a 0,5 e inferior a 0,6.
A partir do texto acima, julgue os itens subseqüentes, considerando que, para avaliar a tese de que a probabilidade foi reduzida para 0,9p, será efetuada uma nova pesquisa com 900 pessoas selecionadas aleatoriamente entre aquelas que sofreram o primeiro infarto do miocárdio no período de cinco anos antes até cinco anos depois da publicação do veto.
Segundo os referidos cientistas italianos, a probabilidade de uma pessoa sofrer o primeiro infarto do miocárdio no período de cinco anos antes até cinco anos depois da publicação do veto é, em média, inferior a 0,9p.
Um estudo de L. Y. Wang et al., publicado no Journal
of Adolescent Health, em 2008, estabeleceu uma relação entre
o índice de massa corporal (x) de uma pessoa na adolescência e
a probabilidade de essa pessoa tornar-se obesa quando adulta, por
meio de um modelo de regressão não-linear na forma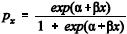
, em que 
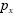representa a probabilidade
esperada de uma pessoa tornar-se obesa na fase adulta, dado que,
na adolescência, a massa corporal era igual a um valor x, e ? e ?
são coeficientes do modelo. Segundo os autores do estudo,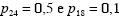
.
Com base nessas informações, julgue os itens de 108 a 110.
A estimação dos coeficientes pode ser feita via máxima verossimilhança, e a estatística de Hosmer-Lemeshow é útil para a verificação da qualidade do ajustamento. Uma avaliação da significância estatística das estimativas encontradas para os coeficientes ? e ? pode ser feita pelo teste de Wald ou pelo teste da razão de verossimilhança.
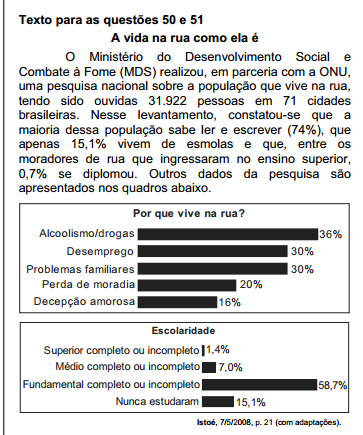
No universo pesquisado, considere que P seja o conjunto
das pessoas que vivem na rua por motivos de
alcoolismo/drogas e Q seja o conjunto daquelas cujo
motivo para viverem na rua é a decepção amorosa.
Escolhendo-se ao acaso uma pessoa no grupo pesquisado
e supondo-se que seja igual a 40% a probabilidade de que
essa pessoa faça parte do conjunto P ou do conjunto Q,
então a probabilidade de que ela faça parte do conjunto
interseção de P e Q é igual a
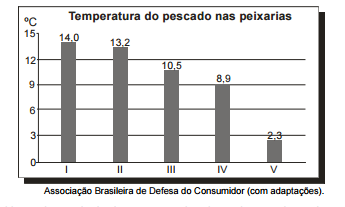
Uma das principais causas da degradação de peixes
frescos é a contaminação por bactérias. O gráfico
apresenta resultados de um estudo acerca da temperatura
de peixes frescos vendidos em cinco peixarias. O ideal é
que esses peixes sejam vendidos com temperaturas entre
2 ºC e 4 ºC. Selecionando-se aleatoriamente uma das
cinco peixarias pesquisadas, a probabilidade de ela vender
peixes frescos na condição ideal é igual a
A queima de cana aumenta a concentração de
dióxido de carbono e de material particulado na atmosfera,
causa alteração do clima e contribui para o aumento de
doenças respiratórias. A tabela abaixo apresenta números
relativos a pacientes internados em um hospital no período
da queima da cana.
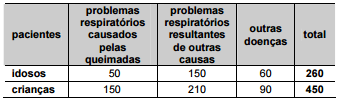
Escolhendo-se aleatoriamente um paciente internado
nesse hospital por problemas respiratórios causados pelas
queimadas, a probabilidade de que ele seja uma criança é
igual a
Um time de futebol amador ganhou uma
taça ao vencer um campeonato. Os jogadores
decidiram que o prêmio seria guardado na casa de
um deles. Todos quiseram guardar a taça em suas
casas. Na discussão para se decidir com quem
ficaria o troféu, travou-se o seguinte diálogo:
Pedro, camisa 6: — Tive uma idéia. Nós
somos 11 jogadores e nossas camisas estão
numeradas de 2 a 12. Tenho dois dados com as
faces numeradas de 1 a 6. Se eu jogar os dois
dados, a soma dos números das faces que ficarem
para cima pode variar de 2 (1 + 1) até 12 (6 + 6).
Vamos jogar os dados, e quem tiver a camisa com
o número do resultado vai guardar a taça.
Tadeu, camisa 2: — Não sei não... Pedro
sempre foi muito esperto... Acho que ele está
levando alguma vantagem nessa proposta...
Ricardo, camisa 12: — Pensando bem...
Você pode estar certo, pois, conhecendo o Pedro,
é capaz que ele tenha mais chances de ganhar que
nós dois juntos...
Desse diálogo conclui-se que
A tabela ao lado indica a posição
relativa de quatro times de futebol na
cIassificação geral de um torneio, em dois
anos consecutivos. O símbolo ? significa
que o time indicado na linha ficou, no ano
de 2004, à frente do indicado na coluna. O
símbolo * significa que o time indicado na
linha ficou, no ano de 2005, à frente do
indicado na coluna.
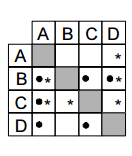
A probabilidade de que um desses quatro times, escolhido ao
acaso, tenha obtido a mesma classificação no torneio, em 2004 e
2005, é igual a
