Para o sorteio de amigo secreto, Maria gostaria de tirar uma menina. Sabendo que todos os 42 alunos de sua sala participariam e que contando com ela, a população de meninas era o dobro da população de meninos, quais as chances de Maria tirar como amigo secreto um menino?
As 20 vagas de um estacionamento são organizadas em 4 fileiras de 5 vagas cada, sendo as vagas da primeira fileira numeradas de um a cinco [1 a 5], da segunda fileira de seis a dez [6 a 10] e assim sucessivamente. Quatro veículos entram no estacionamento vazio. A probabilidade de que os quatros veículos estacionem em vagas numeradas com números primos, e em fileiras distintas é
Os indivíduos S1, S2, S3 e S4, suspeitos da prática de um ilícito penal, foram interrogados, isoladamente, nessa mesma ordem. No depoimento, com relação à responsabilização pela prática do ilícito, S1 disse que S2 mentiria; S2 disse que S3 mentiria; S3 disse que S4 mentiria.
A partir dessa situação, julgue o item a seguir.
Considerando que a conclusão ao final do interrogatório tenha sido a de que apenas dois deles mentiram, mas que não fora possível identificá-los, escolhendo-se ao acaso dois entre os quatro para novos depoimentos, a probabilidade de apenas um deles ter mentido no primeiro interrogatório é superior a 0,5.
Um agente de fiscalização e orientação visitou sete escolas, quatro empresas e três laboratórios. Depois, apresentou um relatório de fiscalização para cada estabelecimento que visitou.
Com base nessa situação hipotética, julgue o item a seguir.
Sabendo-se que a metade dos relatórios apresentaram problemas nos estabelecimentos visitados, então a probabilidade de haver problema em algum relatório referente a uma escola é maior que 99%.
Várias pessoas, entre as quais Artur e Mário, estão sentadas em volta de uma mesa redonda. Entre Artur e Mário há 3 pessoas por um lado e 5 pessoas pelo outro.
Uma das pessoas da mesa é sorteada ao acaso.
A probabilidade de que essa pessoa sorteada não seja nem Artur, nem Mário, nem nenhum dos seus vizinhos, é de
Ao sortear duas cartas consecutivamente e sem reposição em um baralho completo, qual é a probabilidade de serem retirados um oito de copas e um seis de ouro? (Considerar o baralho completo com 52 cartaz e cada naipe com 13 cartaz)
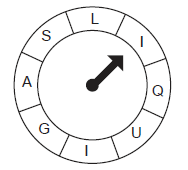
A Figura a seguir mostra um jogo eletrônico no qual, a cada jogada, a seta, após ser girada, para, aleatoriamente e com igual probabilidade, em qualquer uma das oito casas com as letras da palavra LIQUIGÁS.
Um jogador só é vencedor se, em duas jogadas consecutivas, a seta apontar para letras iguais.
A probabilidade de um jogador ser vencedor, fazendo apenas duas jogadas, é igual a
Uma aposta é feita em um jogo de sorte. Um jogador para ganhar a rodada final terá que atirar uma moeda e um dado é jogado. O jogador ganhará a premiação se o resultado da rodada for cara para a moeda e ser o número 4 no dado. Marque a alternativa que apresenta a probabilidade aproximada do jogador ganhar a rodada.
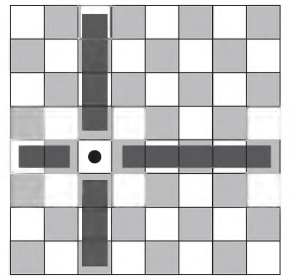
Um designer de jogos planeja um jogo que faz uso de um tabuleiro de dimensão n x n, com n > 2 , no qual cada jogador, na sua vez, coloca uma peça sobre uma das casas vazias do tabuleiro. Quando uma peça é posicionada, a região formada pelas casas que estão na mesma linha ou coluna dessa peça é chamada de zona de combate dessa peça. Na figura está ilustrada a zona de combate de uma peça colocada em uma das casas de um tabuleiro de dimensão 8 x 8.
O tabuleiro deve ser dimensionado de forma que a probabilidade de se posicionar a segunda peça aleatoriamente, seguindo a regra do jogo, e esta ficar sobre a zona de combate da primeira, seja inferior a 1/5.
A dimensão mínima que o designer deve adotar para esse tabuleiro é
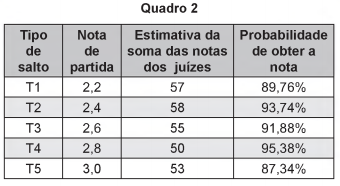
O salto ornamental é um esporte em que cada competidor realiza seis saltos. A nota em cada salto é calculada pela soma das notas dos juízes, multiplicada pela nota de partida (o grau de dificuldade de cada salto). Fica em primeiro lugar o atleta que obtiver a maior soma das seis notas recebidas.
O atleta 10 irá realizar o último salto da final. Ele observa no Quadro 1, antes de executar o salto, o recorte do quadro parcial de notas com a sua classificação e a dos três primeiros lugares até aquele momento.
Ele precisa decidir com seu treinador qual salto deverá realizar. Os dados dos possíveis tipos de salto estão no Quadro 2.
O atleta optará pelo salto com a maior probabilidade de obter a nota estimada, de maneira que lhe permita alcançar o primeiro lugar.
Considerando essas condições, o salto que o atleta deverá escolher é o de tipo
A probabilidade de ocorrer certo evento é dada por:
Acerca da probabilidade, analise as afirmativas a seguir:
I. Experimento aleatório: são experimentos que, quando repetidos em condições iguais, podem fornecer resultados diferentes. Por exemplo, o lançamento de um dado é um experimento aleatório, pois, cada vez que o dado é jogado pode-se obter um número diferente, que antes do lançamento, é desconhecido.
II. Espaço amostral: é o conjunto de todos os resultados possíveis de ocorrer em um experimento aleatório. Por exemplo, o espaço amostral de um dado é o conjunto {1; 2; 3; 4; 5; 6}. Neste conjunto estão todas as possibilidades de resultado de um lançamento.
III. Evento: é o resultado desejado. É um subconjunto do espaço amostral. Por exemplo, o evento “ocorrência de uma face par em um lançamento" é o subconjunto {2; 4; 6}.
Está(ão) CORRETA(s) a(s) afirmativa(s).
Dados os conjuntos A = {1, 2, 3} e B = {4, 5, 6, 7}, João escolhe ao acaso um elemento de cada um deles.
A probabilidade de que o produto dos dois elementos escolhidos seja um número par é:
Um candidato está se preparando para um concurso em que o edital prevê três temas: direito; matemática; e ética. A tabela abaixo aponta seu planejamento de tempo de estudo.
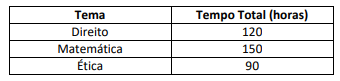
Suponha-se que, para cada tema, o tempo gasto seja proporcional ao conteúdo estudado, por exemplo, com 60 h, ele estuda metade do conteúdo de direito e, com 30 h, um terço do conteúdo de ética. O candidato estudará 6 h por dia de semana e 4 h por dia de fim de semana, começando em uma segunda-feira.
Com base nesse caso hipotético, julgue o item a seguir.
Se, em cada dia, ele escolher aleatoriamente o tema a estudar, então a chance de escolher direito nos dois primeiros dias é maior que 15%.
Numa urna há somente 8 bolas azuis numeradas de 1 a 8 e 12 bolas verdes numeradas de 9 a 20. A probabilidade de sortearmos uma única bola dessa urna e ela ter um número par, sabendo que ela é azul,é