Uma indústria produz uma peça em que uma amostra aleatória de 144 peças apresentou um peso médio igual a 19,5 kg. O desvio padrão da população dos pesos destas peças, considerada de tamanho infinito e normalmente distribuída, é igual a 2 kg. Deseja-se testar a hipótese de que a média µ da população é igual a 20 kg, a um nível de significância a. Foram formuladas as hipóteses  (hipótese alternativa). Considerando que na distribuição normal padrão (Z) as probabilidades
(hipótese alternativa). Considerando que na distribuição normal padrão (Z) as probabilidades 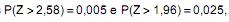 então
então
Sabe-se que a variável aleatória X tem distribuição exponencial com média 0,5. Nessas condições, sua função geratriz de momentos é dada por
As medidas dos comprimentos de uma peça fabricada por uma empresa apresentam uma distribuição normal com desvio padrão desconhecido. Uma amostra aleatória de 9 peças apresentou uma média igual a 85 cm e um desvio padrão igual a 15 cm. Considerando a população de tamanho infinito e 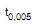 o quantil da distribuição t de Student para teste unicaudal tal que
o quantil da distribuição t de Student para teste unicaudal tal que 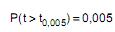 com n graus de liberdade, obteve-se, com base nessa amostra, um intervalo de confiança de 99% para a média populacional. Este intervalo de confiança, em cm, é igual a
com n graus de liberdade, obteve-se, com base nessa amostra, um intervalo de confiança de 99% para a média populacional. Este intervalo de confiança, em cm, é igual a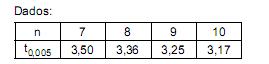
Suponha que o número de eleitores que chegam a uma seção de uma Zona Eleitoral no dia de uma determinada eleição, siga a uma distribuição de Poisson com uma média de chegada de 30 eleitores por meia hora. A probabilidade de que cheguem menos de 3 eleitores em 5 minutos é
Sobre conceitos de análise multivariada, analise.
I. O expoente da função de densidade normal univariada pode ser generalizada para o caso multivariado, com um vetor 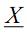 de observações (p x 1):
de observações (p x 1): 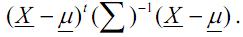
II. A função de distribuição qui-quadrado pode ser expressa por uma função gama incompleta.
III. Uma das propriedades da distribuição normal multivariada é a de que, dado um vetor normalmente distribuído, combinações lineares dos componentes desse vetor não serão normalmente distribuídos.
Assinale

