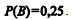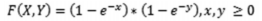A média de uma variável aleatória X, cuja distribuição é desconhecida, é igual a m, com m > 0. Pelo Teorema de Tchebichev, a probabilidade de X não pertencer ao intervalo (m − θ, m + θ), com m > θ, é no máximo igual a 16%. O desvio padrão de X é então igual a θ multiplicado por
A reforma trabalhista de 2017 estabelece limites para indenizações recebidas por dano extrapatrimonial na Justiça do Trabalho, ou seja, danos de caráter subjetivo tais como os danos morais, por exemplo. Em um Tribunal do Trabalho, o valor das indenizações, X, pode ser modelado por uma distribuição de probabilidades segundo uma função densidade de probabilidade do tipo f(x) = 3x2, para 0 < x < 1. Para determinar o valor da indenização em reais, o valor resultante de X deve ser multiplicado por R$ 100 mil.
Se 10 indenizações são observadas, o valor esperado, em reais e desprezando-se os centavos, da segunda maior indenização é dado, em R$, por
Se F(x) possui dominância estocástica de primeira ordem sobre G(x), então, no plano probabilidade-retorno, o gráfico de F estará sempre abaixo do gráfico de G.
Em determinado tribunal, a probabilidade de extinção de um processo judicial com julgamento de mérito é
e a probabilidade de extinção de um processo judicial sem julgamento de mérito é 
em que os eventos são eventos 
mutuamente excludentes e denotam, respectivamente, os eventos complementares dos eventos A e B.
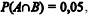
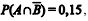
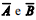
Com referência a essa situação hipotética, julgue o item que se segue.
Os jogadores X e Y lançam um dado honesto, com seis faces numeradas de 1 a 6, e observa-se a face superior do dado. O jogador X lança o dado 50 vezes, e o jogador Y, 51 vezes.
A probabilidade de que o jogador Y obtenha mais faces com números ímpares do que o jogador X, é:
Em um jogo, os jogadores escolhem três números inteiros diferentes, de 1 a 10. Dois números são sorteados e se ambos estiverem entre os três números escolhidos por um jogador, então ele ganha um prêmio. O sorteio é feito utilizando-se uma urna com 10 bolas numeradas, de 1 até 10, e consiste na retirada de duas bolas da urna, de uma só vez, seguida da leitura em voz alta dos números nelas presentes.
Qual é a probabilidade de um jogador ganhar um prêmio no sorteio do jogo?
Para responder à questão de estatística, considere a Tábua III a seguir:
Seja X uma distribuição Binomial com parâmetros n=5 e p=0,4, qual a probabilidade aproximada de X assumir os valores 2 e 4, respectivamente?
Assinale a alternativa certa sobre a relação das funções de densidade de probabilidade.
Assinale a alternativa correta sobre a densidade dada a seguir.
Numa população muito grande, 50% das pessoas são do sexo feminino. Se 5 pessoas dessa população forem aleatoriamente escolhidas, a probabilidade de que pelo menos 4 delas sejam do sexo feminino é igual a
Em uma pequena clínica hospitalar, a receita diária R e a despesa diária D, ambas em R$ mil, são variáveis aleatórias contínuas, tais que:
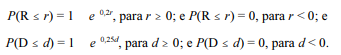
Considerando que a covariância entre as variáveis R e D seja igual a 10, e que
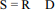seja o saldo diário, julgue o item a seguir.
O saldo diário esperado é E(S) = 0,05.
Em uma pequena clínica hospitalar, a receita diária R e a despesa diária D, ambas em R$ mil, são variáveis aleatórias contínuas, tais que:
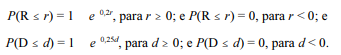
Considerando que a covariância entre as variáveis R e D seja igual a 10, e que
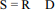seja o saldo diário, julgue o item a seguir.
A correlação linear entre as variáveis aleatórias R e S é igual a 0,5.
Um paciente que compre, mensalmente, determinado medicamento pode optar pelos fornecedores A ou B. Suponha que, em cada mês t(t= 1, 2, 3, ...), essa opção seja feita de acordo com um processo de Markov de primeira ordem: denotada por {Z}, em que, no mês t, Zt = 1, se o paciente optar pelo fornecedor A, ou Zt = 0, se ele optar pelo fornecedor B.
Na matriz
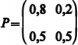, cada entrada Pij, i, j = 0 ou 1 representa a probabilidade de transição do estado i no instante t 1 para o estado j no instante t.
Com base nessas informações, julgue o item a seguir.
Se, nos meses 13 e 14, o paciente tiver optado pelo fornecedor B, então a probabilidade de ele optar novamente pelo fornecedor B no mês 15 é inferior a 0,49.
Responda às questões 50, 51 e 52, com base no texto abaixo. Considere duas urnas contendo as mesmas quantidades de bolas, com a mesma proporção de cores, 3 bolas grenás e 2 verdes. Transfere-se aleatoriamente uma bola de uma urna para a outra. Em seguida, sortea-se uma bola da urna que passou a ter uma bola a mais.
A probabilidade de ter saído a bola grená na primeira extração,
sabendo-se que saiu bola verde na segunda extração é de:
Na tabela a seguir, estão listados os possíveis retornos
de um projeto de investimentos e as respectivas
probabilidades de ocorrências desses retornos:
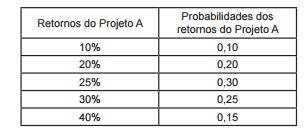
O retorno médio esperado do Projeto A é igual a
