Uma determinada indústria produz três produtos. A produção total é 1.000 unidades por mês.
O controle de qualidade da indústria registrou os seguintes números de peças defeituosas na produção:
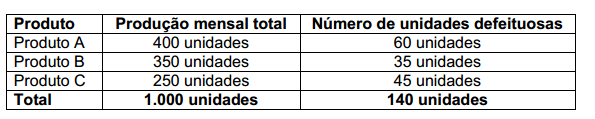
A probabilidade de encontrar uma peça defeituosa do produto B é de:
Uma sociedade empresária apresentou as seguintes estimativas de vendas de computadores:
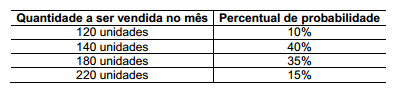
A quantidade esperada de unidades a serem vendidas no mês é de:
Em uma pescaria, os pescadores Alberto, Bruno e Carlos colocavam os peixes que pescavam em um mesmo recipiente. Ao final da pescaria, o recipiente continha 16 piaus e 32 piaparas. Na divisão dos peixes, cada um deles afirmou que teria pescado mais peixes que os outros dois.
Julgue o item a seguir, a respeito dessa situação.
Na situação dada, se 2 peixes fossem retirados do recipiente, aleatoriamente, a probabilidade de que pelo menos um fosse um piau seria maior que 1⁄2.
Com base nos conceitos de probabilidade, julgue os itens seguintes.
Considere três eventos (A, B e C), de modo que A depende de B, mas não de C, e B depende de C. Nessa situação, se P(A ∩ B ∩ C) = sub, sup { font-size: 0.6em;} 1⁄4, P(B) = sub, sup { font-size: 0.6em;} 3⁄5 e P(C) = sub, sup { font-size: 0.6em;} 5⁄8 então P(A | B) = sub, sup { font-size: 0.6em;} 2⁄3.
De uma distribuição com média 100 e variância 25 são coletados 225 valores independentes (amostra). Denotando-se a média amostral por M e considerando a aproximação
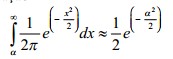
a probabilidade de que |M-80| < 1 é
Num lote de rodas para automóveis, sabe–se que 8 não apresentam defeitos e as 4 restantes apresentam defeitos. A probabilidade de se escolher aleatoriamente duas rodas e elas não serem defeituosas é de:
Considere os eventos A, B, C e D, definidos abaixo, relativos ao
número de veículos por família em determinada cidade.
A = uma família possui 1 ou mais veículos;
B = uma família possui 2 ou mais veículos;
C = uma família possui 3 ou mais veículos;
D = uma família possui 4 ou mais veículos.
Considere, ainda, que as probabilidades de ocorrência desses
eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com
base nessas informações, julgue os itens que se seguem.
Os eventos A e D são independentes.
Atenção: Para resolver às questões de números 38 a 40, use, dentre as informações dadas a seguir, as que julgar apropriadas.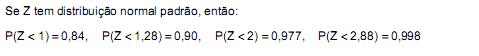 
Seja X uma variável aleatória normal multivariada com vetor de médias e matriz de covariâncias dadas, respectivamente, por: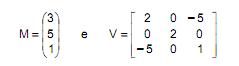 
Seja a variável aleatória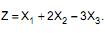 
Nessas condições, P(3 < Z < 17) é igual a
Seja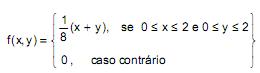 
a função densidade de probabilidade da variável aleatória bidi- mensional contínua (X,Y). A esperança condicional de Y dado que X vale 1, denotada
por E(Y | X = 1), é igual a
Sabe-se que A, B e C são eventos independentes, associados a um mesmo espaço amostral, com probabilidades dadas, respectivamente, por 1/3 e 1/5, 1/2 . A probabilidade de que exatamente dois desses eventos ocorram é igual a
Considere os eventos A, B, C e D, definidos abaixo, relativos ao
número de veículos por família em determinada cidade.
A = uma família possui 1 ou mais veículos;
B = uma família possui 2 ou mais veículos;
C = uma família possui 3 ou mais veículos;
D = uma família possui 4 ou mais veículos.
Considere, ainda, que as probabilidades de ocorrência desses
eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com
base nessas informações, julgue os itens que se seguem.
A probabilidade condicional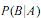 
é inferior a 0,6.
Considere os eventos A, B, C e D, definidos abaixo, relativos ao
número de veículos por família em determinada cidade.
A = uma família possui 1 ou mais veículos;
B = uma família possui 2 ou mais veículos;
C = uma família possui 3 ou mais veículos;
D = uma família possui 4 ou mais veículos.
Considere, ainda, que as probabilidades de ocorrência desses
eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com
base nessas informações, julgue os itens que se seguem.
A probabilidade de uma família na referida cidade possuir exatamente 1 veículo é igual a 0,3.
Atenção: Para resolver às questões de números 38 a 40, use, dentre as informações dadas a seguir, as que julgar apropriadas.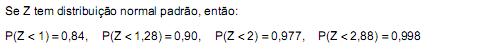 
Considere as variáveis aleatórias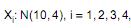 
, independentes. Seja 
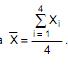Nessas condições, o valor a tal que 
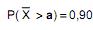é igual a
A função densidade de probabilidade da variável aleatória X é dada por: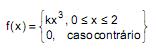 
A probabilidade condicional dada por: P(1 ≤ X ≤ 1,5 
X < 1,5) é igual a
Em um grupo de 20 bolas, 5 são vermelhas e 15 verdes. A probabilidade, com aproximação de duas casas decimais, de que sejam retiradas três bolas vermelhas em sequência, sem reposição, é
