O técnico da seleção brasileira de vôlei de praia dispõe de um grupo de N pessoas para participar de uma olimpíada, mas uma pessoa teve que deixar o grupo. Sendo assim, para uma partida de vôlei de praia o número de duplas possíveis que este técnico pode formar com as pessoas que ficaram no grupo é igual a 21 duplas. Então, o número de pessoas inicialmente no grupo era de:
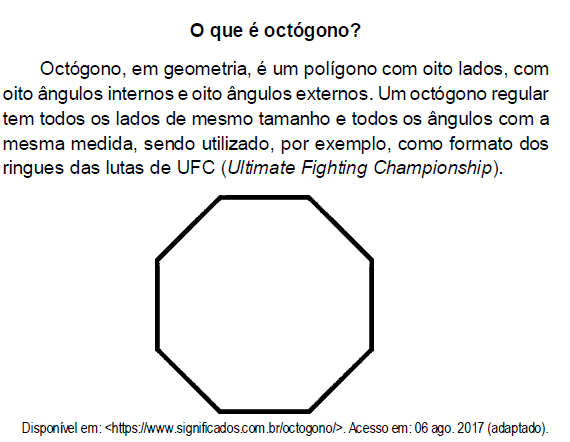
Aplicando-se os princípios de contagem, infere-se que o número de diagonais de um octógono regular é igual a
Qual a probabilidade de um candidato desse concurso, ao resolver as cinco questões de raciocínio lógico matemático, com cinco opções cada questão, acertar exatamente quatro questões?
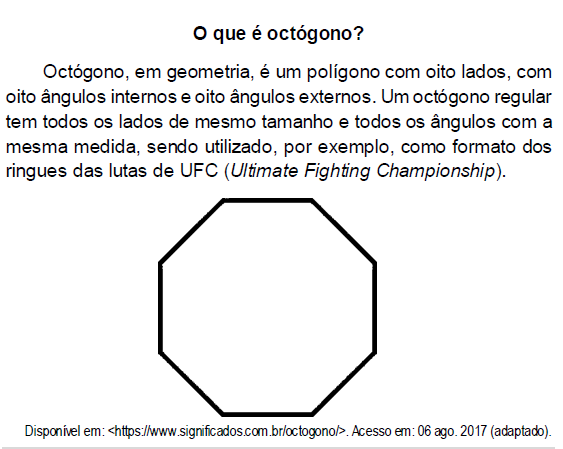
Aplicando-se os princípios de contagem, infere-se que o número de diagonais de um octógono regular é igual a
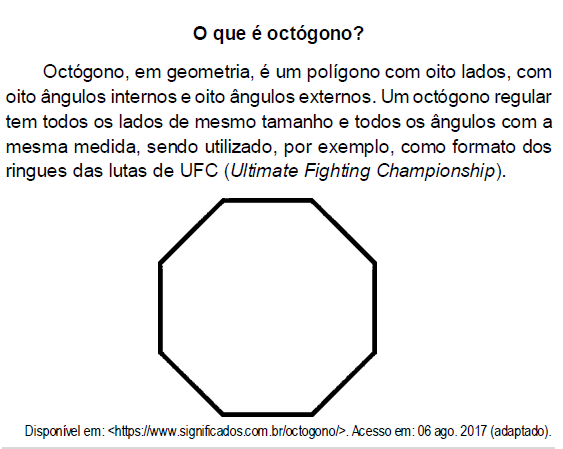
Aplicando-se os princípios de contagem, infere-se que o número de diagonais de um octógono regular é igual a
O Presidente da Comissão de um Concurso decide que agora cada comissão de fiscalização será composta por três fiscais. Se, para um determinado concurso existem dez fiscais, quantas comissões podem ser formadas com esses fiscais?
A prova do concurso interno para Sargento de um grupamento foi composta por 40 questões, com 5 alternativas diferentes de respostas para cada questão Quantos são os possíveis gabaritos dessa prova?
Um professor montará uma prova com as 4 questões que eledispõe. O número de maneiras diferentes que o professor podemontar essa prova, levando em conta apenas a ordem dasquestões, é
O comitê organizador da Copa do Mundo 2014 criou a logomarca da Copa, composta de uma figura plana e o slogan "Juntos num só ritmo", com as mãos que se unem formando a taça Fifa. Considere que o comitê organizador resolvesse utilizar todas as cores da bandeira nacional (verde, amarelo, azul e branco) para colorir a logomarca, de forma que regiões vizinhas tenham cores diferentes.
De quantas maneiras diferentes o comitê organizador da Copa poderia pintar a logomarca com as cores citadas?
Assinale a alternativa que apresenta quantos números de 4 algarismos maiores que 5000 pode-se formar, com os algarismos 0, 1, 2, 4, 7 e 8.
Com relação aos anagramas da palavra ITAIPU, identifique como verdadeiras V ou falsas F as seguintes afirmativas:
( ) Há 360 anagramas distintos.
( ) Há 30 anagramas distintos em que as duas consoantes estão juntas.
( ) Há 24 anagramas que começam e terminam com a letra I.
( ) Há 200 anagramas em que as letras I estão separadas.
Assinale a alternativa que apresenta a sequência correta, de cima para baixo.
Com a palavra CONSELHO, é possível formar mais de 700 anagramas que comecem e terminem com O.
Uma sorveteria dispõe de 5 sabores diferentes de sorvete de massa. O total de maneiras distintas que se pode saborear um sorvete com duas bolas, considerando que as bolas podem ser do mesmo sabor, é:
Uma equipe com seis analistas deve ser formada a partir de um grupo de dez analistas previdenciários (entre eles Marcos e Gabriel). O número total de equipes que se pode formar, se Marcos e Gabriel devem necessariamente fazer parte, é:
Antônio Alves utiliza como senha para seu computador as cinco letras de seu sobrenome, fora da ordem original. Assinale a alternativa que indica quantas possibilidades de senha são possíveis de obter desta forma.