Na auditoria de uma empresa, o auditor concluiu que:
“Ocorreu desvio de recursos se, e somente se, o gerente financeiro
e o presidente da empresa estiveram envolvidos nesse desvio".
Considerando que a conclusão do auditor corresponde a uma
proposição verdadeira, julgue os itens seguintes.
Considere que a proposição-conclusão do auditor possa ser escrita, simbolicamente, na forma P↔Q∧R, em que P, Q e R sejam proposições adequadamente escolhidas. Nesse caso, a negação da proposição-conclusão do auditor estará corretamente escrita na forma [(~P)∧(QvR)]∧[~(QvR)∧P].
Considere a expressão a seguir.
{(A → B) ∧ (C → A)} → (C → B)
Essa expressão é
O salário por hora de pedreiro é de $7,00 e do seu auxiliar é de $3,00. Juntos eles receberam $53,00 por um determinado trabalho. O pedreiro trabalhou um período de tempo diferente do trabalhado pelo auxiliar. Se eles tivessem recebido um dólar a menos por hora, teriam recebido $42,00. A quantidade de horas trabalhadas pelo pedreiro e pelo auxiliar foi, respectivamente,
Considere que os termos da sucessão seguinte foram obtidos segundo determinado padrão.
Se, de acordo com o padrão estabelecido, X e Y são o décimo e o décimo terceiro termos dessa sucessão, então a razão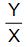 
é igual a
De um grupo de 100 pessoas, 30 leem semanalmente uma revista de notícias, 48 leem diariamente um jornal impresso e 22 leem ambos. Selecionando ao acaso uma pessoa do grupo, se ela lê a revista qual a probabilidade de ler o jornal ?
Caso ou compro uma bicicleta. Viajo ou não caso. Vou morar em Pasárgada ou não compro uma bicicleta. Ora, não vou morar em Pasárgada. Assim,
Sabe-se que exatamente quatro dos cinco grupos de letras abaixo têm uma característica comum.
BCFE - HILK - JKNM - PQTS - RSUV
Considerando que a ordem alfabética adotada é a oficial, o único grupo de letras que NÃO apresenta a característica comum dos demais é:
Proposições são sentenças que podem ser julgadas como verdadeiras — V — ou falsas — F —, de forma que um julgamento exclui o outro, e são simbolizadas por letras maiúsculas, como P, Q, R e S. A partir de proposições conhecidas, novas proposições podem ser construídas usando-se símbolos especiais. Alguns desses símbolos são apresentados na tabela abaixo.
A negação da referida proposição é a proposição {[(PvQ)v[(~R)vS]}v{[(~P)w(~S)]↔(~Q)v(~R)]}.
Proposições são sentenças que podem ser julgadas como verdadeiras — V — ou falsas — F —, de forma que um julgamento exclui o outro, e são simbolizadas por letras maiúsculas, como P, Q, R e S. A partir de proposições conhecidas, novas proposições podem ser construídas usando-se símbolos especiais. Alguns desses símbolos são apresentados na tabela abaixo.
Se P e S forem V e Q e R forem F, então o valor lógico da proposição em questão será F.
Amanda é médica ginecologista e, durante os fi nais de semana, ela recebe, em média, 2 chamadas por hora em seu telefone celular. Assim, a probabilidade de, no próximo final de semana, Amanda receber exatamente 3 chamadas em 2 horas é igual a:
Um tipo de argumento dedutivo em que a conclusão (Q) é consequência necessária de premissas (P1 e P2) é um silogismo. Com base nessa definição, considere os argumentos a seguir.
I. P1: Alguns gatos de olhos verdes são brancos.
P2: Pepe é um gato de olhos verdes.
Q : Pepe é um gato branco.
II. P1: Todo aluno que resolveu os exercícios foi aprovado.
P2: Lucas foi aprovado.
Q : Lucas resolveu os exercícios.
III. P1: Todos os animais aquáticos têm duas asas.
P2: A vaca é um animal aquático.
Q : A vaca tem duas asas.
IV. P1: Todos os moradores do oitavo andar são engenheiros.
P2: Albano mora no oitavo andar.
Q : Albano é engenheiro.
Assinale a alternativa correta.
Se não chove, então o cachorro late. Se chove, então o papagaio não fala. Entretanto, o papagaio está falando. Logo,
Qual é o capital no qual uma taxa de 13% foi aplicada resultando R$ 52.000,00 de porcentagem?
Se Paulo é irmão de Ana, então Natália é prima de Carlos. Se Natália é prima de Carlos, então Marta não é mãe de Rodrigo. Se Marta não é mãe de Rodrigo, então Leila é tia de Maria. Ora, Leila não é tia de Maria. Logo
Se Ana é pianista, então Beatriz é violinista. Se Ana é violinista, então Beatriz é pianista. Se Ana é pianista, Denise é violinista. Se Ana é violinista, então Denise é pianista. Se Beatriz é violinista, então Denise é pianista. Sabendo-se que nenhuma delas toca mais de um instrumento, então Ana, Beatriz e Denise tocam, respectivamente:
