Em uma pesquisa, os dados foram coletados e organizados conforme a tabela apresentada.
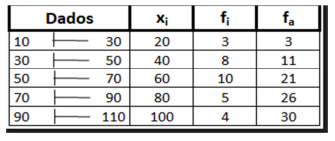
A mediana dos dados agrupados é
Considere verdadeiras as proposições a seguir:
I. Todo atleta é homem.
II. Nenhum homem sabe lavar roupa.
Assinale a alternativa que apresenta uma conclusão correta.
Considere verdadeiras as quatro afirmações a seguir:
I. Ou Nicole é professora, ou Rodolfo não é atuário.
II. Se Miguel é musicista, então Camila não é museóloga.
III. Se Nicole é professora, então Camila é museóloga.
IV. Rodolfo é atuário.
Assim, pode-se concluir corretamente que:
Um torneio de futebol de mesa reuniu seis moradores de um condomínio (Carlos, Elias, Jorge, Wilson, Bruno e Robson). Na primeira sequência, três jogos aconteceram simultaneamente. Antes de iniciar o torneio, três torcedores tentaram descobrir quais seriam os três vencedores nas partidas que seriam realizadas, não necessariamente na ordem destes jogos.
Torcedor 1: Carlos, Bruno e Elias;
Torcedor 2: Bruno, Wilson e Robson;
Torcedor 3: Elias, Jorge e Robson.
Nessa sequência de jogos iniciais, o adversário direto do Carlos foi:
Numa pesquisa sobre o consumo de dois sabores de suco, 200 pessoas foram entrevistadas. Dessas, 144 disseram consumir suco de laranja, 136 disseram consumir suco de uva e 18 disseram não consumir nenhum desses sabores de suco. De acordo com essa pesquisa, quantos dos entrevistados consomem os dois sabores de suco (laranja e uva)?
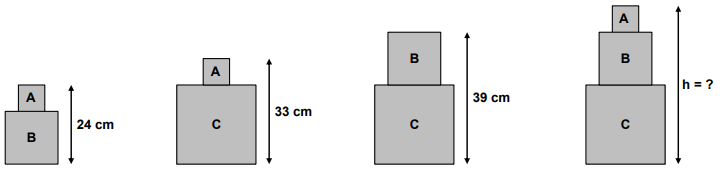
A sequência a seguir ilustra o empilhamento de caixas A, B e C.
Nessas condições, a altura h, da última pilha, é:
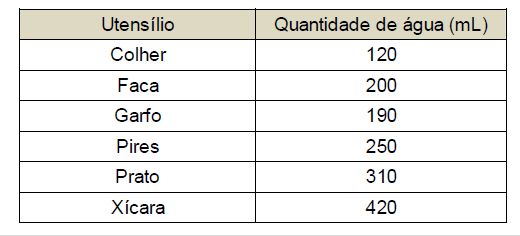
Para controlar o consumo de água de sua residência, uma dona de casa estimou as quantidades de água utilizadas nas lavagens dos utensílios utilizados no café da manhã, tendo obtido os dados apresentados na tabela.
Considerando esses dados, numa ocasião em que foram lavados três colheres, duas facas, três garfos, três pires, dois pratos e três xícaras, o consumo de água foi de
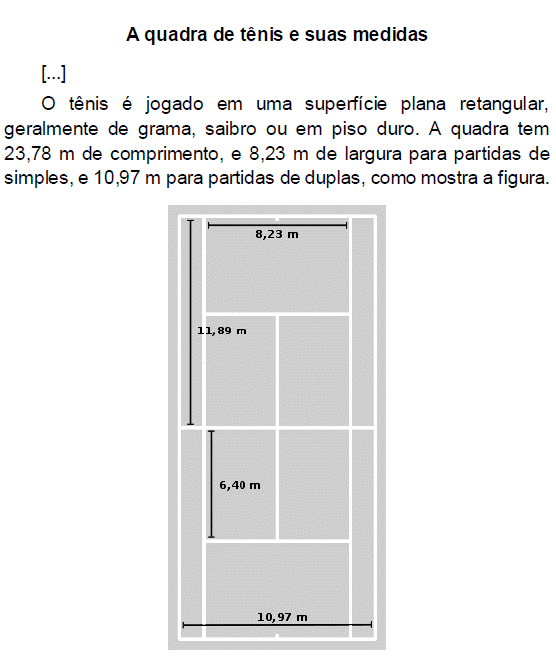
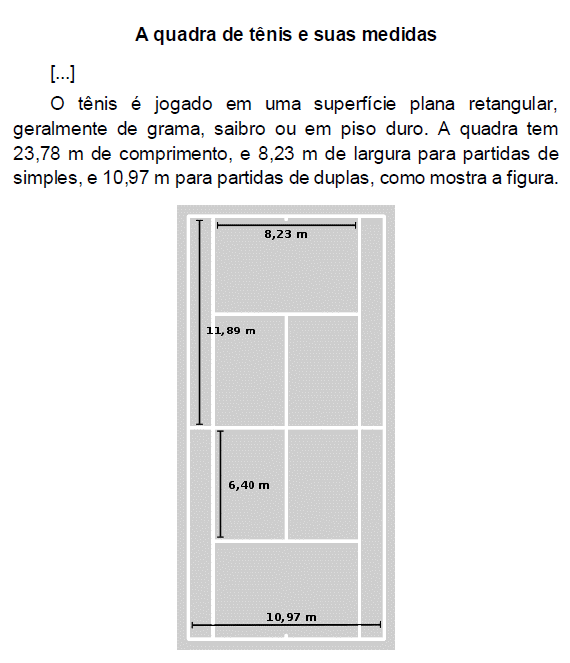
Dadas as afirmativas sobre essas dimensões,
I. A razão entre o comprimento da quadra para partidas de simples e a largura para partidas de simples é menor que a razão entre o comprimento da quadra para partidas de duplas e a largura para partidas de duplas.
II. A razão entre as áreas da quadra para partidas de duplas e para partidas de simples é igual à razão entre as larguras da quadra para partidas de duplas e para partidas de simples.
III. A razão entre as diagonais da quadra para partidas de duplas e para partidas de simples é igual à razão entre os comprimentos da quadra para partidas de duplas e para partidas de simples.
verifica-se que está(ão) correta(s)
Uma pesquisa de opinião entrevistou 37 clientes em um supermercado, quanto à sua preferência pelos sabores morango e laranja, de um suco recém-lançado. Dos entrevistados, 22 gostaram do suco de morango, 19 gostaram do de laranja e 3 não quiseram provar os sucos. Quantos clientes entrevistados gostaram dos dois sabores do suco?
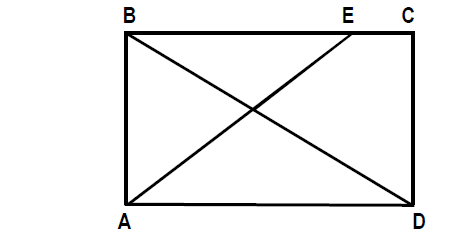
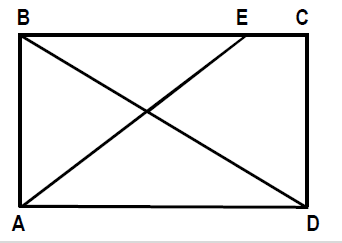
A figura, desenhada sem escala, apresenta o projeto de uma praça retangular com 30 m de largura (AB) e 40 m de comprimento (AD), tendo dois passeios BD e AE, para circulação de pedestres, com E situado a 10 m de C.
Se desprezarmos as larguras das calçadas e dos passeios e adotarmos √2 = 1,4, qual é, em metros, o comprimento do passeio AE?
A figura, desenhada sem escala, apresenta o projeto de uma praça retangular com 30 m de largura (AB) e 40 m de comprimento (AD), tendo dois passeios BD e AE, para circulação de pedestres, com E situado a 10 m de C.
Se desprezarmos as larguras das calçadas e dos passeios e adotarmos 
Um trabalho extraclasse foi realizado em grupos compostos por seis alunos. Para apresentar esse trabalho, o professor irá selecionar, de forma aleatória, dois alunos desse grupo.
De quantas maneiras esse professor poderá escolher dois alunos para a apresentação?
Observe o produto a seguir.
A8 x 3B = 3.430
As letras A e B representam dois algarismos diferentes situados na sequência de 1 a 9.
Os números A e B são, respectivamente:
A figura, desenhada sem escala, apresenta o projeto de uma praça retangular com 30 m de largura (AB) e 40 m de comprimento (AD), tendo dois passeios BD e AE, para circulação de pedestres, com E situado a 10 m de C.
Se desprezarmos as larguras das calçadas e dos passeios e adotarmos √2 = 1,4, qual é, em metros, o comprimento do passeio AE?
Dadas as afirmativas sobre essas dimensões,
I. A razão entre o comprimento da quadra para partidas de simples e a largura para partidas de simples é menor que a razão entre o comprimento da quadra para partidas de duplas e a largura para partidas de duplas.
II. A razão entre as áreas da quadra para partidas de duplas e para partidas de simples é igual à razão entre as larguras da quadra para partidas de duplas e para partidas de simples.
III. A razão entre as diagonais da quadra para partidas de duplas e para partidas de simples é igual à razão entre os comprimentos da quadra para partidas de duplas e para partidas de simples.
verifica-se que está(ão) correta(s)