Em uma sala de espera da Defensoria Pública, 20 pessoas estão aguardando o atendimento. São brasileiros, todos naturais da região sudeste do país.
Supondo que o local de nascimento dessas pessoas seja aleatório, a probabilidade de que os três primeiros a serem atendidos tenham nascido em diferentes unidades da federação é igual a:
Um grupo de telefonista é constituído por cinco mulheres e três homens. Três telefonistas são selecionados ao acaso, a probabilidade de que ao menos um deles sejam mulher é:
Em uma visita ao teatro do Sesc, há 800 pessoas, das quais: 280 são homens; 400 são mulheres que já praticaram teatro; e 60 são homens que não praticaram teatro, Ao se escolher aleatoriamente uma pessoa, escolhe-se um homem. Sendo assim, a probabilidade de ele já ter praticado teatro é igual a
As 6 vagas da garagem de um pequeno edifício recém-construído serão sorteadas entre os proprietários dos 6 apartamentos, de modo que cada apartamento terá direito a uma vaga. As vagas ficam localizadas lado a lado ao longo de uma parede. Dois irmãos, proprietários dos apartamentos 1 e 2, gostariam que suas vagas ficassem localizadas lado a lado. A probabilidade de que isso aconteça é igual a
Em um gabinete, há seis computadores distintos disponíveis e três pessoas para os utilizarem. Dois deles são muito mais rápidos que os outros e sempre serão escolhidos para uso caso estejam vagos. Todos possuem uma senha formada por quatro algarismos, ordenados dentro do conjunto {0, 1, 2,..., 9}. Em cada senha, nenhum algarismo é repetido.
Com base nesse caso hipotético, julgue o seguinte item.
Se uma senha de um computador é conhecida e outro computador possui senha com os mesmos algarismos, então a chance de acertá-la ao acaso é menor que 2%.
Sobre a probabilidade, analise as afirmativas a seguir:
I. A probabilidade de ocorrer um evento A ou um evento B é a probabilidade de ocorrer um elemento de A, mais a probabilidade de ocorrer um elemento de B, menos a probabilidade de ocorrer um elemento comum a A e B.
II. O que se diz no item I é que: P(A ∪ B) = P( A ) + P( B ) - P(A ∩ B).
III. Dois eventos são mutuamente exclusivos se não possuírem elementos em comum. A união dos eventos se reduz a: P(A ∪ B) = P( A ) × P( B ).
Está(ão) CORRETA(s) a(s) afirmativa(s).
Nesse final de semana, 2 dos 40 soldados do batalhão em que Renato é lotado deverão ser sorteados para uma missão especial. Para tal, o comandante identificou os soldados com os números de 1 a 40 e colocou 40 bolas numeradas de 1 a 40 em uma urna para retirar duas que corresponderiam aos sorteados. Ao ser retirada, a primeira bola caiu no chão e se perdeu, sem que o respectivo número tenha sido visto. O comandante então decidiu realizar o sorteio com as bolas restantes.
Nessa situação hipotética, qual é a probabilidade de que Renato tenha sido um dos dois sorteados?
Uma empresa oferece passagens para determinado trecho nos turnos da manhã, tarde e noite. São três opções de voos pela manhã, quatro pela tarde e duas pela noite. Quatro conselheiros precisam realizar a viagem pelo trecho no mesmo dia. Carlos e Manoel devem viajar pela manhã, Marcos, pela tarde, e Camila, pela tarde ou pela noite.
Com base nessa situação hipotética, julgue o item a seguir.
Existem 63 possibilidades de compras de voos que satisfazem as necessidades dos quatro conselheiros.
Foi realizada uma campanha de coleta de amostras para identificação de leishmaniose em determinado bairro. Ao longo de seis meses, foram coletadas 3000 amostras de sangue, das quais 540 deram resultado positivo para a doença.
Considerando que uma amostra foi escolhida ao acaso, assinale a alternativa que apresenta a probabilidade desta ser negativa.
Uma urna contém 20 bolas, numeradas de 1 a 20. Qual a probabilidade de retirar-se dessa urna um número par e maior que 10?
Em um aeroporto, 30 passageiros que desembarcaram de determinado voo e que estiveram nos países A, B ou C, nos quais ocorre uma epidemia infecciosa, foram selecionados para ser examinados. Constatou-se que exatamente 25 dos passageiros selecionados estiveram em A ou em B, nenhum desses 25 passageiros esteve em C e 6 desses 25 passageiros estiveram em A e em B.
Com referência a essa situação hipotética, julgue o item seguinte.
Se 2 dos 30 passageiros selecionados forem escolhidos ao acaso, então a probabilidade de esses 2 passageiros terem estado em 2 desses países é inferior a 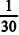
Julgue o próximo item, considerando a proposição P a seguir.
P: "O bom jornalista não faz reportagem em benefício próprio nem deixa de fazer aquela que prejudique seus interesses".
Escolhendo aleatoriamente uma linha da tabela verdade da proposição P, a probabilidade de que todos os valores dessa linha sejam V é superior a 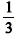
Julgue o próximo item, acerca da seguinte proposição:
P: "A nomeação do novo servidor público ocorre para reposição de vacância em área essencial, ou o candidato aprovado não será nomeado".
Escolhendo aleatoriamente uma linha da tabela verdade da proposição P, a probabilidade de que todos os valores dessa linha sejam F é superior a 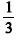
Uma turma de um colégio é formada por 15 rapazes e 25 moças. Dois quintos das moças e um terço dos rapazes dessa turma usam óculos. Um dos 40 estudantes dessa turma foi sorteado, a probabilidade de que a pessoa sorteada (rapaz ou moça) use óculos, é de:
Uma empresa oferece passagens para determinado trecho nos turnos da manhã, tarde e noite. São três opções de voos pela manhã, quatro pela tarde e duas pela noite. Quatro conselheiros precisam realizar a viagem pelo trecho no mesmo dia. Carlos e Manoel devem viajar pela manhã, Marcos, pela tarde, e Camila, pela tarde ou pela noite.
Com base nessa situação hipotética, julgue o item a seguir.
Se o voo de Camila for comprado aleatoriamente, respeitando-se sua necessidade, a chance de ela viajar pela noite é superior a 30%.

