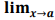Dois dados honestos são jogados. Assim temos que a probabilidade condicional de que pelo menos um deles caia no 6, se os dados caírem em números diferentes é:
Uma pirâmide hexagonal regular, com a aresta da base medindo 8 cm e sua altura 10 cm. Podemos dizer que a apótema da pirâmide é:
Seja um intervalo aberto não-vazio
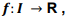
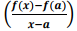
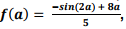
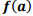
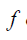
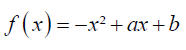
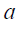
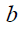
y = f(a) uma função de I em R. Diz-se que função f (a) é
f ' (a) = 
> Nessas condições, dada 
podemos concluir que a derivada
é:
A função 
definida por 
tem valor máximo igual a 4 para X = 1. Então, os valores dos parâmetros reais 
e 
são:
Em uma maratona de matemática, realizada em uma determinada escola foi elaborada uma prova que continha 100 questões. Todas elas deveriam ser respondidas. Cada resposta certa valia 2 pontos, e cada resposta errada valia (-1) ponto. Se um aluno fez 65 pontos, quantas questões ele acertou e quantas ele errou?
Seja S o conjunto dos números pares entre 1 e 9. A quantidade de subconjuntos de é igual a:
Seja
Uma operação policial será realizada com uma equipe de seis agentes, que têm prenomes distintos, entre eles André, Bruno e Caio. Um agente será o coordenador da operação e outro, o assistente deste; ambos ficarão na base móvel de operações nas proximidades do local de realização da operação. Nessa operação, um agente se infiltrará, disfarçado, entre os suspeitos, em reunião por estes marcada em uma casa noturna, e outros três agentes, também disfarçados, entrarão na casa noturna para prestar apoio ao infiltrado, caso seja necessário.
A respeito dessa situação hipotética, julgue o item seguinte.
A quantidade de maneiras distintas de formar a equipe, de modo que André, Bruno e Caio sejam os agentes que ocuparão, respectivamente, as vagas de coordenador, assistente e infiltrado, é superior a 5.
Na preparação de uma ação policial, um agente fez algumas medições em uma casa noturna, mostradas na figura a seguir. O agente, em pé no ponto A, de frente para a casa noturna, estava a 10 m de distância do ponto C, correspondente à porta de entrada da casa noturna. Do ponto B, posição dos olhos do agente, ele visualizava uma câmera de segurança no ponto D, no prédio da casa noturna, segundo um ângulo de visão de 30º com a horizontal. Perpendicularmente a AC, e a 24 m de A, ficava localizada uma base móvel para apoio à operação, no ponto E.
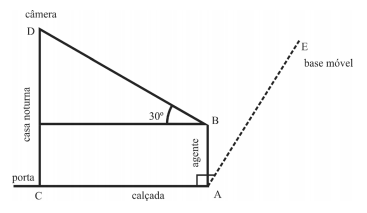
Com referência às informações contidas na situação hipotética e na figura anteriormente apresentadas, julgue o próximo item.
No dia da operação, caso precise evadir-se do estabelecimento pela porta de entrada e chegar ao ponto correspondente à base móvel, um agente que esteja no ponto C precisará se deslocar por, pelo menos, 26 m.
Dadas as afirmativas a respeito de dois números naturais A e B, cada um deles com exatamente duas ordens,
I. A diferença A – B tem apenas uma ordem.
II. O produto A x B tem exatamente quatro ordens.
III. A soma A + B tem exatamente duas ordens ou exatamente três ordens.
verifica-se que está(ão) correta(s)
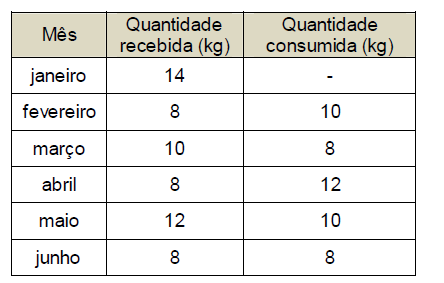
A tabela apresenta as quantidades de arroz recebidas e consumidas no primeiro semestre de 2017 em uma escola que teve suas aulas iniciadas em fevereiro.
De acordo com os dados apresentados, qual o consumo médio mensal de arroz a partir do início das aulas?
Uma escola possui um pátio retangular cujo perímetro mede 84,5 metros. Se o comprimento desse pátio é de 23,9 metros, a altura e a área em centímetros correspondem respectivamente a:
Jorge precisa fazer uma instalação hidráulica com 27 metros de extensão. Considerando que ele usará tubos de PVC e que cada tubo possui 6 metros de comprimento.
A função do segundo grau x² - 5x + 9 = 0 com domínio pertencente ao campo dos reais possui como ponto de vértice, Yv, o ponto de:
Letícia possui 2 pedaços de barbantes, 1 medindo 18m e outro medindo 30m. Sabendo que ela precisa dividir os barbantes em tamanhos iguais, qual será o tamanho de cada pedaço de barbante?
