O Sistema Métrico Decimal é o mais utilizado atualmente para medir comprimentos e distâncias. Em algumas atividades, porém, é possível observar a utilização de diferentes unidades de medida. Um exemplo disso pode ser observado no quadro.
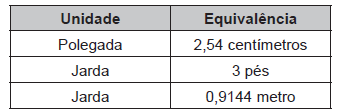
Assim, um pé, em polegada, equivale a
Um aplicativo de relacionamentos funciona da seguinte forma: o usuário cria um perfil com foto e informações pessoais, indica as características dos usuários com quem deseja estabelecer contato e determina um raio de abrangência a partir da sua localização. O aplicativo identifica as pessoas que se encaixam no perfil desejado e que estão a uma distância do usuário menor ou igual ao raio de abrangência. Caso dois usuários tenham perfis compatíveis e estejam numa região de abrangência comum a ambos, o aplicativo promove o contato entre os usuários, o que é chamado de match.
O usuário P define um raio de abrangência com medida de 3 km e busca ampliar a possibilidade de obter um match se deslocando para a região central da cidade, que concentra um maior número de usuários. O gráfico ilustra alguns bares que o usuário P costuma frequentar para ativar o aplicativo, indicados por I, II, III, IV e V. Sabe-se que os usuários Q, R e S, cujas posições estão descritas pelo gráfico, são compatíveis com o usuário P, e que estes definiram raios de abrangência respectivamente iguais a 3 km, 2 km e 5 km.
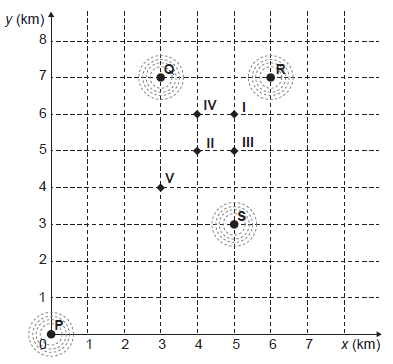
Com base no gráfico e nas afirmações anteriores, em qual bar o usuário P teria a possibilidade de um match com os usuários Q, R e S, simultaneamente?
Para construir uma piscina, cuja área total da superfície interna é igual a 40 m2, uma construtora apresentou o seguinte orçamento:
• R$ 10 000,00 pela elaboração do projeto;
• R$ 40 000,00 pelos custos fixos;
• R$ 2 500,00 por metro quadrado para construção da área interna da piscina.
Após a apresentação do orçamento, essa empresa decidiu reduzir o valor de elaboração do projeto em 50%, mas recalculou o valor do metro quadrado para a construção da área interna da piscina, concluindo haver a necessidade de aumentá-lo em 25%. Além disso, a construtora pretende dar um desconto nos custos fixos, de maneira que o novo valor do orçamento seja reduzido em 10% em relação ao total inicial.
O percentual de desconto que a construtora deverá conceder nos custos fixos é de
Uma empresa de transporte disponibiliza, para embalagem de encomendas, caixas de papelão no formato de paralelepípedo retoretângulo, conforme dimensões no quadro.
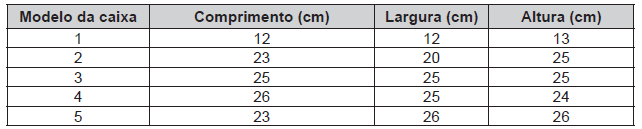
Para embalar uma encomenda, contendo um objeto esférico com 11 cm de raio, essa empresa adota como critério a utilização da caixa, dentre os modelos disponíveis, que comporte, quando fechada e sem deformá-la, a encomenda e que possua a menor área de superfície total.
Desconsidere a espessura da caixa.
Nessas condições, qual dos modelos apresentados deverá ser o escolhido pela empresa?
Na anestesia peridural, como a usada nos partos, o médico anestesista precisa introduzir uma agulha nas costas do paciente, que atravessará várias camadas de tecido até chegar a uma região estreita, chamada espaço epidural, que envolve a medula espinhal. A agulha é usada para injetar um líquido anestésico, e a força que deve ser aplicada à agulha para fazê-la avançar através dos tecidos é variável.
A figura é um gráfico do módulo F da força (em newton) em função do deslocamento x da ponta da agulha (em milímetro) durante uma anestesia peridural típica.
Considere que a velocidade de penetração da agulha deva ser a mesma durante a aplicação da anestesia eque a força aplicada à agulha pelo médico anestesista cada ponto deve ser proporcional à resistência naquele ponto.
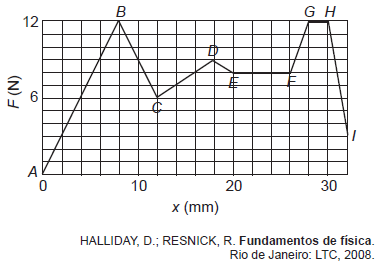
Com base nas informações apresentadas, a maior resistência à força aplicada observa-se ao longo do segmento
Um jardineiro cultiva plantas ornamentais e as coloca à venda quando estas atingem 30 centímetros de altura. Esse jardineiro estudou o crescimento de suas plantas, em função do tempo, e deduziu uma fórmula que calcula a altura em função do tempo, a partir do momento em que a planta brota do solo até o momento em que ela atinge sua altura máxima de 40 centímetros. A fórmula é h = 5·log2 (t + 1), em que t é o tempo contado em dia e h, a altura da planta em centímetro.
A partir do momento em que uma dessas plantas é colocada à venda, em quanto tempo, em dia, ela alcançará sua altura máxima?
Um fiscal de certa empresa de ônibus registra o tempo, em minuto, que um motorista novato gasta para completar certo percurso. No Quadro 1 figuram s tempos gastos pelo motorista ao realizar o mesmo percurso sete vezes. O Quadro 2 apresenta uma classificação para a variabilidade do tempo, segundo o valor do desvio padrão.
Com base nas informações apresentadas nos quadros, a variabilidade do tempo é
O boliche é um esporte cujo objetivo é derrubar, com uma bola, uma série de pinos alinhados em uma pista. A professora de matemática organizou um jogo de boliche em que os pinos são garrafas que possuem rótulos com números, conforme mostra o esquema.
O aluno marca pontos de acordo com a soma das quantidades expressas nos rótulos das garrafas que são derrubadas. Se dois ou mais rótulos representam a mesma quantidade, apenas um deles entra na contagem dos pontos. Um aluno marcou 7,55 pontos em uma jogada. Uma das garrafas que ele derrubou tinha o rótulo 6,8.
A quantidade máxima de garrafas que ele derrubou para obter essa pontuação é igual a
Uma empresa sorteia prêmios entre os funcionários como reconhecimento pelo tempo trabalhado. A tabela mostra a distribuição de frequência de 20 empregados dessa empresa que têm de 25 a 35 anos trabalhados. A empresa sorteou, entre esses empregados, uma viagem de uma semana, sendo dois deles escolhidos aleatoriamente.
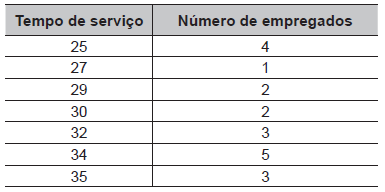
Qual a probabilidade de que ambos os sorteados tenham 34 anos de trabalho?
No ano de 1751, o matemático Euler conseguiu demonstrar a famosa relação para poliedros convexos que relaciona o número de suas faces (F), arestas (A) e vértices (V): V + F = A + 2. No entanto, na busca dessa demonstração, essa relação foi sendo testada em poliedros convexos e não convexos. Observou-se que alguns poliedros não convexos satisfaziam a relação e outros não. Um exemplo de poliedro não convexo é dado na figura. Todas as faces que não podem ser vistas diretamente são retangulares.
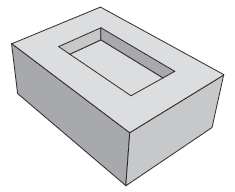
Qual a relação entre os vértices, as faces e as arestas do poliedro apresentado na figura?
O modelo predador-presa consiste em descrever a interação entre duas espécies, sendo que uma delas (presa) serve de alimento para a outra (predador). A resposta funcional é a relação entre a taxa de consumo de um predador e a densidade populacional de sua presa. A figura mostra três respostas funcionais (f, g, h), em que a variável independente representa a densidade populacional da presa.
Qual o maior intervalo em que a resposta funcional f(x) é menor que as respostas funcionais g(x) e h(x), simultaneamente?
No trapézio isósceles mostrado na figura a seguir, M é o ponto médio do segmento BC, e os pontos P e Q são obtidos dividindo o segmento AD em três partes iguais.
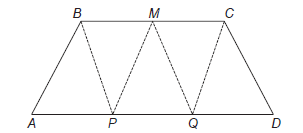
Pelos pontos B, M, C, P e Q são traçados segmentos de reta, determinando cinco triângulos internos ao trapézio, conforme a figura.
A razão entre 
e 
que determina áreas iguais para os cinco triângulos mostrados na figura é
Uma pista circular delimitada por duas circunferências concêntricas foi construída. Na circunferência interna dessa pista, de raio 0,3 km, serão colocados aparelhos de ginástica localizados nos pontos P, Q e R, conforme a figura.
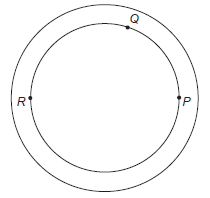
O segmento RP é um diâmetro dessa circunferência interna, e o ângulo 
tem medida igual a 
radianos.
Para uma pessoa ir do ponto P ao ponto Q andando pela circunferência interna no sentido anti-horário, ela percorrerá uma distância, em quilômetro, igual a
O esquema apresenta a concentração de álcool presente em cada 200 mL de diferentes tipos de bebidas.
De acordo com as informações, indique qual o número máximo de taças de vinho, de 300 mL, que podem ser consumidas, semanalmente, por uma mulher que se enquadre no grupo de médio risco.
Com base nas informações, qual expressão representa a quantidade de água retirada, em litro por minuto?
