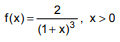Os sinistros de uma companhia de seguros (em R$ milhões) são modelados por uma variável aleatória contínua X com função densidade de probabilidade dada por:
A probabilidade de um sinistro, aleatoriamente escolhido, exceder R$ 1,5 milhões é
10% das lâmpadas fabricadas pela empresa A queimam antes de 1000h de funcionamento. Das fabricadas pela empresa B, 5% queima antes de 1000h de funcionamento. Das fabricadas pela empresa C, 1% queima antes de 1000h de funcionamento. Em uma grande loja de varejo, 20% das lâmpadas em estoque são da marca A, 30% são da marca B e 50% são da marca C.
Uma lâmpada é escolhida ao acaso do estoque dessa loja. A probabilidade de que ela não queime antes de 1000h de funcionamento é igual a
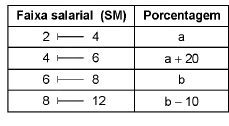
A tabela a seguir apresenta a distribuição de frequências dos salários, em número de salários mínimos (SM), dos funcionários de um órgão público:
Sabe-se que:
b - a = 5%,
é a média salarial, obtida por meio dessa tabela, calculada como se todos os valores de cada faixa salarial coincidissem com o ponto médio da referida faixa,
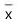
md é a mediana salarial, calculada por meio dessa tabela pelo método da interpolação linear.
Nessas condições,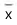 
+ md, em anos, é igual a
Um estudo mostrou que a quantidade mensal Y (em quilogramas) de drogas ilícitas apreendidas em certo local segue uma distribuição exponencial e que a média da variável aleatória Y é igual a 10 kg.
Considerando que F(y) = P(Y ≤ y) represente a função de distribuição de Y, em que y é uma possível quantidade de interesse (em kg), e que 0,37 seja valor aproximado de e-1, julgue os itens subsecutivos.
O desvio padrão da variável aleatória Y é superior a 12 kg.
Um estudo mostrou que a quantidade mensal Y (em quilogramas) de drogas ilícitas apreendidas em certo local segue uma distribuição exponencial e que a média da variável aleatória Y é igual a 10 kg.
Considerando que F(y) = P(Y ≤ y) represente a função de distribuição de Y, em que y é uma possível quantidade de interesse (em kg), e que 0,37 seja valor aproximado de e-1, julgue os itens subsecutivos.
A quantidade 10 kg corresponde ao valor mais provável da distribuição Y de modo que P(Y = 10 kg) ≥ 0,50.
A respeito dessa situação hipotética, julgue o item a seguir.
O coeficiente de explicação do modelo (R2) foi superior a 0,70.
A respeito dessa situação hipotética, julgue o item a seguir.
De acordo com o modelo ajustado, caso a concentração molar de potássio encontrada em uma vítima seja igual a 2 mmol/dm3, o valor predito correspondente do intervalo post mortem será igual a 15 horas.
A Tabela a seguir apresenta a distribuição da variável número de talões de cheques, X, solicitados no último mês de uma amostra de 200 clientes de um banco.
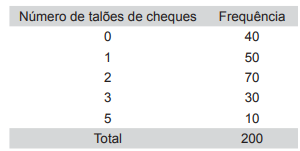
A função de distribuição empírica para a variável X, número de talões de cheques solicitados, é:
Um professor elaborou 10 questões diferentes para uma prova, das quais 2 são fáceis, 5 são de dificuldade média, e 3 são difíceis. No momento, o professor está na fase de montagem da prova. A montagem da prova é a ordem segundo a qual as 10 questões serão apresentadas. O professor estabeleceu o seguinte critério de distribuição das dificuldades das questões, para ser seguido na montagem da prova:
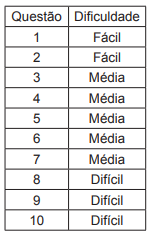
De quantas formas diferentes o professor pode montar a prova seguindo o critério estabelecido?
Seja X uma variável aleatória discreta cuja função distribuição de probabilidade acumulada é dada por:
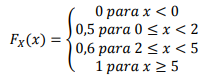
Como consequência, é correto afirmar que:
De um lote de 12 processos, três serão sorteados para fins de avaliação por parte do Conselho Nacional de Justiça (CNJ). Em cinco dos processos originais houve condenação do réu, e nos demais, absolvição.
Assim, a probabilidade de que a maior parte dos processos a serem sorteados seja de absolvições é igual a:
Sabe-se que a probabilidade de condenação em 1ª instância, para certo juízo, é igual a 1/5, enquanto a probabilidade de que a decisão seja alterada por um recurso é igual a 1/3.
Se, em qualquer caso, as partes estão dispostas a recorrer até a 3ª instância, a probabilidade de que haja uma absolvição é:
Para o planejamento de uma pesquisa de campo, do ponto de vista estatístico, existem três aspectos fundamentais a definir, quais sejam: a população alvo, o modo de seleção e o tamanho da amostra.
Esses aspectos estão logicamente interligados e sobre eles é correto afirmar que:
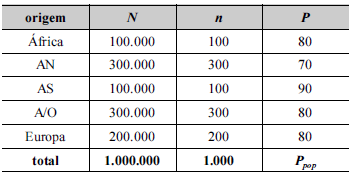
Uma pesquisa realizada com passageiros estrangeiros que se encontravam em determinado aeroporto durante um grande evento esportivo no país teve como finalidade investigar a sensação de segurança nos voos internacionais. Foram entrevistados 1.000 passageiros, alocando-se a amostra de acordo com o continente de origem de cada um — África, América do Norte (AN), América do Sul (AS), Ásia/Oceania (A/O) ou Europa. Na tabela seguinte, N é o tamanho populacional de passageiros em voos internacionais no período de interesse da pesquisa; n é o tamanho da amostra por origem; P é o percentual dos passageiros entrevistados que se manifestaram satisfeitos no que se refere à sensação de segurança.
Em cada grupo de origem, os passageiros entrevistados foram selecionados por amostragem aleatória simples. A última linha da tabela mostra o total populacional no período da pesquisa, o tamanho total da amostra e Ppop representa o percentual populacional de passageiros satisfeitos.
A partir dessas informações, julgue o próximo item.
A estimativa do percentual populacional de passageiros originários da África que se mostraram satisfeitos com a sensação de segurança nos voos internacionais foi igual a 80% e a estimativa do erro padrão associado a esse resultado foi inferior a 4%.
Um estudo mostrou que a quantidade mensal Y (em quilogramas) de drogas ilícitas apreendidas em certo local segue uma distribuição exponencial e que a média da variável aleatória Y é igual a 10 kg.
Considerando que F(y) = P(Y ≤ y) represente a função de distribuição de Y, em que y é uma possível quantidade de interesse (em kg), e que 0,37 seja valor aproximado de e-1, julgue os itens subsecutivos.
P(Y ≥ 10 kg) > P(Y ≤ 10 kg).
