Com o propósito de produzir inferências acerca da
proporção populacional (p) de pessoas satisfeitas com determinado
serviço oferecido pelo judiciário brasileiro, foi considerada uma
pequena amostra de 30 pessoas, tendo cada uma de responder 1,
para o caso de estar satisfeita, ou 0, para o caso de não estar
satisfeita. Os dados da amostra estão registrados a seguir.
0 0 0 1 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 0 1
Com base nessas informações, julgue os itens seguintes.
Caso o p–valor do teste H0: p = 0,5 versus H1: p … 0,5 seja igual
a 0,0295, então, se a hipótese alternativa fosse alterada para
H1: p < 0,5, o teste seria significativo ao nível de significância
de 2%.
Segundo notícia veiculada recentemente, em rede nacional,
os processos do judiciário estão demorando mais que o razoável
porque os juízes têm de analisar, em média, 3 mil processos por
ano. Para verificar o fato, um analista coletou a quantidade de
processos de uma amostra de 10 juízes, estando os resultados
dispostos a seguir (em mil processos por ano).
2 5 4 3 2 2 3 3,5 2,5 5
Com base nessas informações e considerando que μ representa a
média populacional por juiz, julgue os itens subsequentes.
A estatística do teste para se testar se H0: μ = 3 mil possui 8
graus de liberdade, dada a necessidade de se estimarem a
média e o desvio–padrão e sabendo que os dados seguem uma
distribuição normal.
Em um teste de hipóteses bilateral, com nível de significância α, cujas estatísticas de teste calculadas e tabeladas são designadas por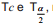 
respectivamente, pode-se afirmar que:
Em um teste de hipótese estatístico sobre um parâmetro, define-se o poder do teste como a
Para testar a existência da regressão por meio do teste t de Student, considerando as hipóteses H0 : ß = 0 (hipótese nula) e
H1 : ß ≠ 0 (hipótese alternativa), obtém-se que o correspondente valor da estatística t (t calculado), para ser comparado com o
respectivo t tabelado, pertence ao intervalo
O valor da estatística utilizada para testar a hipótese de interesse é
Em um determinado ramo de atividade, a população de todos os salários dos empregados é considerada normal e de tamanho infinito. O desvio padrão populacional apresenta um valor igual a R$ 200,00. Deseja−se testar a hipótese H0: = μ = R$ 1.700,00 (hipótese nula) contra H1: μ ≠ R$ 1.700,00 (hipótese alternativa) com base em uma amostra aleatória de tamanho 64 extraída da população (µ é a média da população). A média encontrada para esta amostra apresentou um valor igual a M reais. Fixando o nível de significância do teste em 5% e considerando que na curva normal padrão (Z) as probabilidades P(Z > 1,96) = 0,025 e P(Z > 1,64) = 0,05, H0 não será rejeitada caso
Em uma empresa foram selecionados aleatoriamente 256 empregados que se submeteram a um treinamento durante 30 dias.
Verificando que x empregados apresentaram melhora no desempenho após o treinamento, decidiu-se utilizar o teste do sinal,
atribuindo x sinais positivos para os empregados que melhoraram e (256 - x) sinais negativos para os restantes. Aplicando
então o teste do sinal para decidir se a proporção populacional de sinais positivos (p) é igual a 50%, a um nível de significância
de 5%, foram formuladas as hipóteses H0 : p = 50% (hipótese nula) contra H1 : p ? 50% (hipótese alternativa). Com a
aproximação da distribuição binomial pela normal, sem a correção de continuidade, foi apurado o valor do escore reduzido r
correspondente para comparação com o valor crítico z da distribuição normal padrão Z tal que a probabilidade
P(|Z|≤z ) = 95% . Se r = 2,5, então x é igual a
Um pesquisador testa uma hipótese sobre o valor de um parâmetro da distribuição de probabilidades que descreve a população da qual extraiu uma amostra. O pesquisador define uma estatística S a ser usada no teste, bem como as hipóteses nula H0 e alternativa H1.
Nesse contexto de teste estatístico, verifica-se que o(a)
Em um teste de hipóteses, o intervalo de con?ança obtido para o valor de uma estatística depende do nível de signi? cância adotado. Quanto maior for o intervalo de con?ança, pode-se dizer que:
Lembremos que se X1 , X2 , ... Xn é uma amostra aleatória de uma distribuição uniforme no intervalo (0, θ) e se quisermos testar H0: θ ≤ 1 contra H1: θ > 1, o teste uniformemente mais poderoso de tamanho α rejeitará H se yn > k, em que yn denota a n-ésima estatística de ordem, ou seja, rejeitará H0 se yn = máx {xi} > k. Assim, k é igual a
Com relação a estatística, julgue os itens seguintes.
Suponha que se deseje testar a hipótese nula H0: µ = 5 contra a hipótese alternativa H1: µ > 5, em que µ representa a média populacional em estudo, e que o nível de significância desse teste seja igual a 5%. Nessa situação, será correto efetuar o teste mediante a construção de intervalo de confiança simétrico para a média µ (com 95% de confiança), devendo-se, com base nesse intervalo, rejeitar H0 se o valor 5 estiver abaixo do limite inferior desse intervalo.
Em uma empresa, a quantidade de empregados de uma categoria profissional é igual a 64. Todos eles são submetidos a uma prova e é anotada a nota de cada empregado. Visando melhorar o desempenho destes profissionais, a empresa promove um treinamento para todos eles durante 6 meses. Posteriormente, uma nova prova é aplicada e verifica-se que 41 deles apresentaram melhora e os restantes foram melhores na primeira prova. Utilizou-se o teste dos sinais para decidir se o treinamento funcionou, a um nível de significância de 5%, considerando que ocorreram 41 sinais positivos para os que apresentaram melhora e 23 negativos para os restantes. Sejam as hipóteses H0: p = 0,50 (hipótese nula) e H1: p > 0,50 (hipótese alternativa), em que p é a proporção populacional de sinais positivos. Aproximando a distribuição binomial pela normal, obteve-se o escore reduzido r (sem a correção de continuidade), para ser comparado com o valor crítico z da distribuição normal padrão (Z) tal que a probabilidade P(Z>z) = 0,05. O valor de r é tal que
Com os dados da questão anterior, determine o valor da estatística F para testar a hipótese nula de que o coefi ciente angular da reta do modelo de regressão linear simples de Y em X é igual a zero.
