Observe as sequências abaixo e assinale a alternativa CORRETA:
Uma determinada progressão geométrica de razão 2 possui 10 termos e o último termo é igual a 1.536. Dessa forma, é correto afirmar que a soma dos oito primeiros termos desta progressão é:
Sabendo–se que: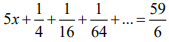 
, o valor de x é:
Assinale a alternativa que apresenta o 9º termo da progressão geométrica abaixo.
21, 42, 84...
Inserem-se, entre os números 1 e 2048, n números reais positivos, de forma que a sucessão obtida seja uma P.G de razão menor que 2. Qual é o menor valor de n?
Considere uma progressão geométrica de termo inicial 4 e razão 3. Qual o sexto termo dessa progressão?
Em uma Progressão Geométrica na qual o 3º termo é 9 e o 7º termo é 33, a soma dos 10 primeiros termos é
Um estudante de matemática estava no segundo semestre da faculdade quando resolveu comprar uma moto. O preço da moto foi à vista R$ 24.000,00. A única forma de pagamento que o estudante conseguiu foi: uma entrada e mais 5 parcelas distribuídas em uma progressão geométrica. A segunda parcela que o estudante pagou foi de R$ 4.000,00 e a quarta de R$ 1.000,00. Qual valor de entrada o estudante precisou pagar para comprar a moto?
O Triângulo de Sierpinsky é um fractal criado a partir de um triângulo equilátero, da seguinte forma: divide-se cada lado do triângulo ao meio, unem-se estes pontos médios e forma-se um novo triângulo equilátero.
Se continuarmos o processo, quantos triângulos brancos haverá no Estágio 10?
Se x − 1, x + 1, x + 7 são, nessa ordem, os três primeiros termos de uma progressão geométrica, o quarto termo é
Em uma Progressão Geométrica o terceiro termo é 36 e a razão é igual a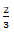 
. O primeiro termo dessa sequência é:
Para interpolar 3 meios geométricos entre 6 e 14.406, a razão deve ser:
O valor do número real b para o qual existe uma progressão geométrica cuja soma dos n primeiros termos, para qualquer número inteiro positivo n, é igual a 3n+1 + b é
Sendo uma progressão geométrica dada por ( 32, α, 8, x, 2, b, 1/2) e uma progressão aritmética dada por (1, x, y, w, 13). Assinale a alternativa que apresente o valor da soma x, y e W.
O lado de um triângulo equilátero mede 3 cm, unindo-se os pontos médios de seus lados obtém-se um novo triângulo equilátero. Unindo-se os pontos médios dos lados do novo triângulo obtém-se outro triangulo equilá-tero. Fazendo isso sucessivamente, determine a soma do perímetro de todos os triângulos que serão formados.
