Com relação a uma sequência numérica a 1, a2, …, an, julgue o item subsequente.
Se a sequência for uma progressão geométrica (PG), em que a1 = 5 e a4 = 135, então a razão dessa PG será maior que 4.
O quinto e o sétimo termos de uma PG (progressão geométrica) de razão positiva valem, respectivamente, 4 e 16. O sexto termo dessa PG é:
A figura a seguir ilustra a primeira etapa de um processo recursivo que, a partir de um hexágono regular em que os lados medem 1 cm de comprimento, constroem-se 6 novos hexágonos regulares.
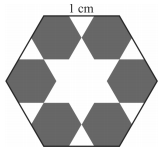
Nesse processo, os lados do hexágono externo são divididos em 3 partes iguais e, conforme mostra a figura, são construídos outros 6 hexágonos regulares; em cada um deles, o comprimento dos lados é igual a 1/3 cm. Na segunda etapa, dividem-se os lados desses 6 novos hexágonos em 3 partes iguais, e constroem-se, de maneira semelhante à primeira etapa, outros 36 hexágonos regulares. Esse processo pode seguir indefinidamente.
Nessa situação, sabendo-se que, se o comprimento dos lados de um hexágono regular for igual a
L cm, a área desse hexágono será igual a 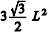
Analise a progressão geométrica abaixo:
(1,2,4,12,24)
Com base nisso, determine a soma dos 10 primeiros termos da PG:
O número de frutas vendidas na barraca de André triplicou a cada dia nos últimos seis dias do ano, ou seja, vendeu x dúzias no 1º dia e a partir do 2º dia, o número de frutas vendidas foi o triplo do dia anterior.
Se o total de frutas vendidas, nos seis dias, foi 8.736 frutas, a quantidade de dúzias vendidas por André, no 1º dia, foi:
Em uma Progressão Geométrica o terceiro termo é 36 e a razão é igual a 
Em uma Progressão Geométrica o terceiro termo é 36 e a razão é igual a 
Em uma Progressão Geométrica o terceiro termo é 36 e a razão é igual a 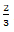
Considere a sequência numérica cujo termo geral é dado por an=21-3n, para n ≥ 1.
Essa sequência numérica é uma progressão
Qual é o sexto termo da progressão geométrica a seguir: (3,−6. . . )?
Considere a seguinte sequência:
Quais termos devem ser removidos para que essa sequência se torne uma progressão geométrica, de razão 2 e termo inicial 3?
Em um laboratório, uma colônia com 5.000 bactérias foi colocada em observação. Notou-se que, a cada 45 minutos, a quantidade de bactérias parecia triplicar. Supondo corretas as observações dos cientistas, quantas bactérias haveria após 6 horas de observação?
Em uma progressão geométrica crescente, a diferença entre os dois primeiros termos é 40 e a razão (q) vale metade do primeiro termo. Nessas condições, o produto entre o primeiro termo e a razão é
Em uma Progressão Geométrica o terceiro termo é 36 e a razão é igual a 
Os três primeiros termos de uma Progressão Geométrica crescente são indicados por 


