A Mega-Sena é um jogo de apostas no qual são sorteadas 6 dentre 60 bolas numeradas de 1 a 60. Cecília fez uma aposta, escolhendo os números 1, 2, 3, 4, 5 e 6. Cecília está acompanhando o sorteio e viu que as três primeiras bolas sorteadas foram as de número 1, 2 e 3.
A chance de Cecília acertar os seis números e ganhar na Mega-Sena é agora de uma em
Em um batalhão de bombeiros, estão de plantão doze soldados, sendo sete homens e cinco mulheres. Desse total de soldados, dois serão escolhidos ao acaso para compor uma equipe que atuará em uma missão.
Nessa situação hipotética, a probabilidade de que essa equipe tenha pelo menos uma mulher é de
Cada um dos itens a seguir apresenta uma situação hipotética seguida de uma assertiva a ser julgada com base em análise combinatória, probabilidade, operações com conjuntos e problemas geométricos.
Considere que 44 servidores falem uma ou mais línguas estrangeiras e que, entre eles, 12 servidores falem apenas inglês; 10 falem apenas espanhol; 11 falem apenas francês; 1 fale inglês e francês; 2 falem espanhol e francês; e 17 falem francês. Nessa situação, 7 servidores falam inglês e espanhol, mas não falam francês.
Ao realizar o cadastro em um aplicativo de investimentos, foi i solicitado ao usuário que criasse uma senha, sendo
permitido o uso somente dos seguintes caracteres:
• algarismos de 0 a 9;
• 26 letras minúsculas do alfabeto;
• 26 letras maiúsculas do alfabeto;
• 6 caracteres especiais !, @, #, $, , &.
Três tipos de estruturas para senha foram apresentadas ao usuário:
• tipo I: formada por quaisquer quatro caracteres
distintos, escolhidos dentre os permitidos;
• tipo II: formada por cinco caracteres distintos,
iniciando por três letras, seguidas por um algarismo
e, ao final, um caractere especial;
• tipo III: formada por seis caracteres distintos, iniciando
por duas letras, seguidas por dois algarismos e, ao
final, dois caracteres especiais.
Considere p1, p2 e p3 as probabilidades de se descobrirem ao acaso, na primeira tentativa, as senhas dos tipos I, II e III, respectivamente.
Nessas condições, o tipo de senha que apresenta a menor probabilidade de ser descoberta ao acaso, na primeira tentativa, é o
Numa sala há 25 carteiras dispostas em 5fileiras com 5 carteiras cada numeradas daseguinte forma: Na primeira fila as carteiras vão
de número 1 a 5, na segunda fileira as carteiras vão de 6 a 10, na terceira fileira as carteiras vão de 11 a 15, na quarta fileira as carteiras vão de 16 a 20 e na última fileira as carteiras vão de 21 a 25.
Nessas condições, a probabilidade de uma pessoa estar sentada numa carteira de número par, sabendo que essa carteira não é da terceira fileira, é igual a:
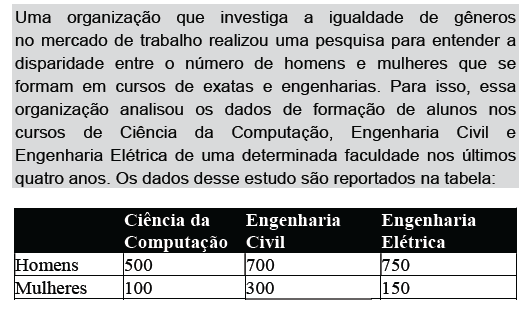
Dadas as afirmativas com relação aos dados coletados,
I. A taxa de pessoas do sexo feminino formadas no curso de Ciência da Computação é de 20%.
II. Apenas 22% das pessoas formadas nesses três cursos são do sexo feminino.
III. A chance de uma pessoa desse grupo, sorteada ao acaso, ser mulher, formada em Ciência da Computação, ou mulher, formada em Engenharia Elétrica, é de apenas 10%.
IV. O curso de Engenharia Civil forma, proporcionalmente, menos mulheres do que homens na comparação entre os três cursos.
verifica-se que estão corretas apenas
O gestor constatou que 3 agentes de pesquisa por telefone, A, B e C, foram responsáveis por 20%, 50% e 30%, respectivamente, do volume total de informação coletada durante um dia. Esses agentes costumam apresentar inconsistência de 20%, 5% e 2%, respectivamente, entre as informações coletadas e as prestadas pelos informantes. Escolheu-se aleatoriamente uma informação coletada e verificou-se que era inconsistente. A probabilidade de ter sido coletada pelo agente A é, aproximadamente, igual a:
Na tabela a seguir, estão os dados de 74 funcionários do setor de comunicação de uma empresa, quanto ao gênero e ao consumo ou não de café:
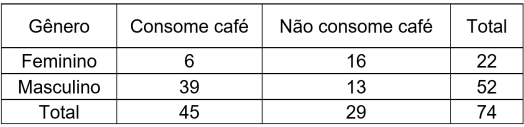
Se um funcionário desse setor for sorteado, a probabilidade de que este consuma café, sabendo que é do gênero feminino, é igual a:
Numa escola houve problemas de segurança. A sala, que presenciou o problema, possui 30 alunos que são testemunhas, sendo 20 meninos e 10 meninas. Se uma testemunha é escolhida aleatoriamente, assinale a alternativa que apresenta qual é a probabilidade dela ser uma menina, aproximadamente.
Em um jogo de cartas, temos somente 3 cartas de copas, 4 cartas de ouros, 6 cartas de
espadas e 7 cartas de paus. Assinale a alternativa que apresenta qual é a probabilidade de retirar uma carta de ouros.
No alojamento de uma universidade, há alguns quartos com o padrão superior ao dos demais. Um desses quartos ficou disponível, e muitos estudantes se candidataram para morar no local. Para escolher quem ficará com o quarto, um sorteio será realizado. Para esse sorteio, cartões individuais com os nomes de todos os estudantes inscritos serão depositados em uma urna, sendo que, para cada estudante de primeiro ano, será depositado um único cartão com seu nome; para cada estudante de segundo ano, dois cartões com seu nome; e, para cada estudante de terceiro ano, três cartões com seu nome. Foram inscritos 200 estudantes de primeiro ano, 150 de segundo ano e 100 de terceiro ano. Todos os cartões têm a mesma probabilidade de serem sorteados.
Qual a probabilidade de o vencedor do sorteio ser um estudante de terceiro ano?
Em uma competição esportiva, o time A enfrentará o time B quatro vezes seguidas. Em cada uma das partidas, a probabilidade de que o time A vença o time B é 0,6.
A probabilidade de que o time A vença apenas duas vezes é de
Numa tarde de domingo Thay e Cris estavam se divertindo com um jogo de tabuleiro. O jogo consistia no lançamento de dois sólidos geométricos, sendo um cubo (hexaedro regular com 6 faces quadradas) e um dodecaedro regular (12 faces pentagonais regulares), numerados de 1 à respectiva quantidade de faces. Ao lançar os sólidos, Thay disse: Se a soma das faces voltadas para cima for um número quadrado perfeito, eu vencerei o jogo! Cris então respondeu: Ok, porém se a soma das faces voltadas para cima for um número primo, quem vencerá sou eu. Analisando o exposto, assinale a alternativa correta.
Marcelo joga, simultaneamente, dois dados cúbicos honestos cujas faces estão numeradas de 1 a 6.
A probabilidade de os dois números sorteados serem consecutivos é:
Gabriela comprou um novo carro que pode ser abastecido tanto com gasolina, álcool ou com os dois. Sabe-se que Gabriela abastece sempre uma vez por semana, que abastece apenas com gasolina um terço das vezes, somente com álcool metade das vezes, e com uma mistura dos dois um sexto das vezes.
A probabilidade de ela ter abastecido com alguma quantidade álcool hoje é de:

