Um carpinteiro guarda, em quatro caixas opacas (não transparentes), dois tipos de parafusos que se diferenciam apenas por suas tonalidades (claros e escuros). Ele sabe exatamente quantos parafusos de cada tipo há em cada caixa. As quantidades estão apresentadas a seguir.
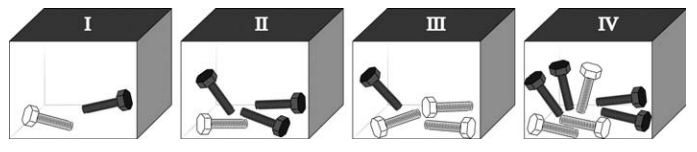
Considere que esse carpinteiro queira retirar, sem olhar, um parafuso de uma de suas caixas, esperando ter a maior probabilidade de obter um de cor clara.
A retirada deve ser feita da caixa
Com a finalidade de motivar seus funcionários, uma empresa premia o funcionário do mês organizando um sorteio de brindes. O sorteio é feito colocando-se em um globo não transparente: 3 bolas vermelhas, 5 bolas azuis, 8 bolas amarelas e 4 bolas brancas. O funcionário do mês deve retirar uma bola ao acaso e seu prêmio será determinado de acordo com a cor da bola: a bola vermelha corresponde a um televisor; a bola azul, a uma bicicleta; a bola amarela, a um ventilador; e a bola branca, a um micro-ondas.
Qual é a probabilidade de o funcionário do mês ganhar um televisor?
Em uma sala de aula, entre alunos e alunas, há 36 pessoas.
Se, em determinado dia, seis das alunas faltarem às aulas e
todos os alunos se fizerem presentes, então, nesse dia, a
quantidade de alunos será o dobro da de alunas. Um
problema que se coloca é determinar quantos alunos e
quantas alunas pertencem a essa sala.
A respeito dessa situação hipotética, julgue os itens
subsecutivos.
Considerando-se que a diretora da escola resolva sortear
um ingresso para teatro entre todos os membros dessa
sala, a probabilidade de que uma das seis alunas faltosas
seja a premiada é superior a 0,15
João fez uma aposta com Maria da seguinte forma: ele escolherá cinco números inteiros diferentes, de 1 a 10; em seguida, sortearão três números diferentes destes dez números. Se os três números sorteados estiverem dentre os escolhidos por João ele vence, caso contrário, Maria vence. Assinale a alternativa que indica a probabilidade de Maria vencer a aposta.
Em uma caixa de medicamentos há 3 medicamentos do tipo A, 2 medicamentos do tipo B e 5 medicamentos do tipo C. Um medicamento é retirado ao acaso da caixa. Assinale a alternativa que indica a probabilidade de o medicamento retirado ser do tipo C.
Numa caixa existem 20 bolas numeradas de 1 a 20. Retirando uma bola ao acaso, a probabilidade de ser par ou múltiplo de 5 é:
A probabilidade de se sortear um número múltiplo de 5 de uma urna que contém 40 bolas numeradas de 1 a 40, é:
Dos 10 médicos habilitados para primeiros-socorros, 6 são homens, e 4, mulheres. Para montagem de uma equipe com 3 médicos sorteados aleatoriamente, qual a probabilidade de os sorteados serem do mesmo sexo?
Um baralho perfeitamente embaralhado e constituído de 52 cartas, sendo 4 naipes (espadas, paus, copas e ouros) e 13 cartas por naipe (ás, 2, 3, 4, 5, 6, 7, 8, 9,10, valete, dama e rei). Considere ás como carta de valor 1, valete como 11, dama como 12 e rei como 13. A probabilidade da soma das duas primeiras cartas retiradas ser igual a 3 está numa faixa.
Em uma reunião estão presentes 6 homens e 4 mulheres. Escolhendo-se ao acaso 3 dessas 10 pessoas, a probabilidade de serem escolhidas 3 pessoas do mesmo sexo é de:
Considere que, num determinado setor da ANAC, três
pessoas, A, B e C, são responsáveis diariamente pelos
relatórios das atividades desenvolvidas. Dos últimos 200
relatórios, A foi o responsável por 50, B foi responsável
por 70 e C foi responsável por 80. Em 6% das vezes, o
relatório de A apresenta algum tipo de erro, de B em 10%
das vezes e de C em 5% das vezes. Seleciona-se ao acaso
um relatório desses 200 e verifica-se que apresenta algum
tipo de erro, então a probabilidade de ter sido elaborado
por B é igual a
José deseja fazer um teste para praticar seus
conhecimentos sobre probabilidade. Ele jogou um
dado comum de seis faces por três vezes e, por
pura “sorte", nas três vezes o dado parou com a
face de número 5 voltada para cima. Calculando a
probabilidade disso acontecer, ele obteve, na forma
fracionária:
José deseja fazer um teste para praticar seus conhecimentos sobre probabilidade. Ele jogou um dado comum de seis faces por três vezes e, por pura “sorte”, nas três vezes o dado parou com a face de número 5 voltada para cima. Calculando a probabilidade disso acontecer, ele obteve, na forma fracionária:
Uma população de 1.000 pessoas acima de 60 anos de
idade foi dividida nos seguintes dois grupos:
A: aqueles que já sofreram infarto (totalizando 400 pessoas); e
B: aqueles que nunca sofreram infarto (totalizando 600 pessoas).
Cada uma das 400 pessoas do grupo A é ou diabética ou
fumante ou ambos (diabética e fumante).
A população do grupo B é constituída por três conjuntos
de indivíduos: fumantes, ex-fumantes e pessoas que nunca fumaram
(não fumantes).
Com base nessas informações, julgue os itens subsecutivos.
Se, no grupo B, a quantidade de fumantes for igual a 20% do
total de pessoas do grupo e a quantidade de ex-fumantes for
igual a 30% da quantidade de pessoas fumantes desse grupo,
então, escolhendo-se aleatoriamente um indivíduo desse grupo,
a probabilidade de ele não pertencer ao conjunto de fumantes
nem ao de ex-fumantes será inferior a 70%.
Considere a seguinte informação para responder a próxima questão: a Prefeitura do Município de São Paulo (PMSP) é subdividida em 32 subprefeituras e cada uma dessas subprefeituras administra vários distritos.
A tabela a seguir, relativa ao ano de 2010, mostra as populações dos quatro distritos que formam certa região administrativa do município de São Paulo.
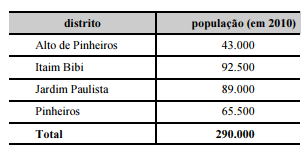
Considerando-se a tabela apresentada, é correto afirmar que, se, em 2010, um habitante dessa região administrativa tivesse sido selecionado ao acaso, a chance de esse habitante ser morador do distrito Jardim Paulista seria

