A probabilidade de um assistente viajar é P(A)= 1/5, a de um técnico em contabilidade viajar é P(C)= 1/4 e a de um técnico em informática viajar é P(I)= 1/3.
A probabilidade de ao menos um deles viajar é:
Dos 10 administradores do CFO, 4 serão escolhidos para compor a comissão de licitação de compras diversas. A comissão terá um presidente, um vice-presidente, um secretário e um auditor, não podendo haver acúmulo de cargos. Jonas é um desses 10 administradores.
Com base nesse caso hipotético, julgue o item que se segue.
Considere-se que tenham sido listadas todas as possíveis comissões e que cada uma delas tenha sido escrita em um pedaço de papel, dobrado e colocado em uma urna para uma escolha aleatória. Nesse caso, a probabilidade de se escolher uma comissão em que Jonas não ocupe nenhum dos 4 cargos é superior a 65%.
O gerente de uma empresa sabe que 70% de seus funcionários são do sexo masculino e foi informado de que a porcentagem de empregados fumantes nessa empresa é de 5% dos homens e de 5% das mulheres. Selecionando, ao acaso, a ficha de cadastro de um dos funcionários, verificou tratar-se de um fumante.
Qual a probabilidade de esse funcionário ser do sexo feminino?
Alberto é um supersticioso e, em todos os carros da sua família, as placas possuem apenas as letras A ou B. Cada placa possui três letras.
Com base nessa situação hipotética e em conhecimentos correlatos, julgue o próximo item.
Escolhendo‐se, ao acaso, uma placa que contenha apenas as letras A ou B, a probabilidade de haver duas letras B e uma letra A será maior que 50%.
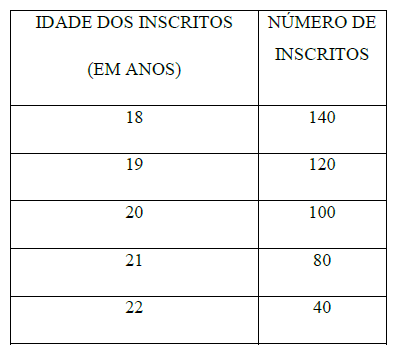
A tabela abaixo apresenta dados coletados nas inscrições dos candidatos de um concurso, de acordo com a idade de cada um.
Se escolhermos aleatoriamente apenas um desses candidatos, a probabilidade de ele ter 21 ou 22 anos é:
Para ganhar um prêmio, uma pessoa deverá retirar, sucessivamente e sem reposição, duas bolas pretas de uma mesma urna.
Inicialmente, as quantidades e cores das bolas são como descritas a seguir:
• Urna A - Possui três bolas brancas, duas bolas pretas e uma bola verde;
• Urna B - Possui seis bolas brancas, três bolas pretas e uma bola verde;
• Urna C - Possui duas bolas pretas e duas bolas verdes;
• Urna D - Possui três bolas brancas e três bolas pretas.
A pessoa deve escolher uma entre as cinco opções apresentadas:
• Opção 1 - Retirar, aleatoriamente, duas bolas da urna A;
• Opção 2 - Retirar, aleatoriamente, duas bolas da urna B;
• Opção 3 - Passar, aleatoriamente, uma bola da urna C para a urna A; após isso, retirar, aleatoriamente, duas bolas da urna A;
• Opção 4 - Passar, aleatoriamente, uma bola da urna D para a urna C; após isso, retirar, aleatoriamente, duas bolas da urna C;
• Opção 5 - Passar, aleatoriamente, uma bola da urna C para a urna D; após isso, retirar, aleatoriamente, duas bolas da urna D.
Com o objetivo de obter a maior probabilidade possível de ganhar o prêmio, a pessoa deve escolher a opção
Um grupo de estudantes do Colégio DELTA recebe forte estímulo para a participação, no final do ano letivo de 2018, em diversas Olimpíadas intelectuais. Há uma previsão de que 44 estudantes participem da Olimpíada de Matemática, 38 na de Física e 26 em ambas. Por outro lado, do grupo, os demais 14 estudantes participarão de outras Olimpíadas. Uma vez confirmada a participação dos estudantes nas olimpíadas em foco, é correto afirmar que a probabilidade de estudantes do grupo participarem de apenas uma das olimpíadas de Matemática ou Física é
Em uma população formada por indivíduos que se encontram empregados, observa-se que 40% deles têm um salário superior a 10 salários mínimos. Para desenvolver um estudo, é extraída uma amostra aleatória de 3 indivíduos desta população com reposição. A probabilidade de que mais que 1 indivíduo desta amostra não tenha um salário superior a 10 salários mínimos é de
Dois tabuleiros de xadrez serão utilizados para a criação de um jogo de sorteio. Inicialmente as linhas e as colunas desses tabuleiros foram numeradas conforme a figura 1. Em seguida, cada casa do tabuleiro será associada ao número que é a soma dos números da linha e da coluna dessa casa. Participarão do sorteio 5 pessoas, e cada uma delas deverá escolher uma das casas do tabuleiro. Em seguida, outra pessoa, chamada juiz, que não tenha visto a escolha dos 5 jogadores, deverá escolher, no outro tabuleiro, uma casa qualquer e realizar a soma da linha e da coluna relativas a essa casa. Será considerado ganhador aquele que tenha escolhido a casa cuja soma do número da linha com o número da coluna coincida com a soma do número da linha com o número da coluna da escolha do juiz.
Se os 5 jogadores escolherem as casas indicadas pelas letras A, B, C, D e E, conforme a figura 2, o jogador que tem maior probabilidade de vencer o sorteio é o que escolher a casa com a letra
Um procedimento muito comum em provas objetivas de concursos, quando o candidato não consegue resolver uma determinada questão, é “escolher aleatoriamente" uma das opções possíveis.
Se o candidato sabe resolver a questão, então ele tem 100% de chance de escolher a opção correta.
Considere um exame em que, para cada questão, existem quatro opções de resposta e apenas uma delas é a correta. Um determinado candidato sabe 70% das respostas desse exame e respondeu corretamente a uma determinada questão.
A probabilidade de este candidato ter “escolhido aleatoriamente" a opção correta dessa questão é
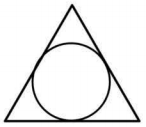
Qual é a probabilidade de se tomar um ponto randomicamente no interior do triângulo equilátero de lado igual a 3cm, situar-se no interior da circunferência inscrita? Assinale a alternativa que apresenta esta probabilidade.
Em um lote com 250 peças, foi constatado que existem exatamente seis defeituosas. Retirando-se, ao acaso, uma peça desse lote, a probabilidade de que ela seja perfeita é de _____%.
Em uma caixa há 15 pilhas, numeradas de 1 a 15. As pilhas que possuem numeração maior que 8 estão carregadas, e as que possuem numeração menor que 9 estão descarregadas. Retirando-se ao acaso uma pilha da caixa, a probabilidade de ela estar descarregada ou ser de numeração ímpar é de:
Imagine uma figura onde está representado um círculo com um quadrado inscrito. Escolhendo, ao acaso, um ponto do círculo a probabilidade desse ponto pertencer ao quadrado é?
Imagine uma figura onde está representado um círculo com um quadrado inscrito. Escolhendo, ao acaso, um ponto do círculo a probabilidade desse ponto pertencer ao quadrado é?